Pattern-Based Approach to the Workflow Satisfiability Problem with User-Independent Constraints
Paper and Code
Feb 22, 2018
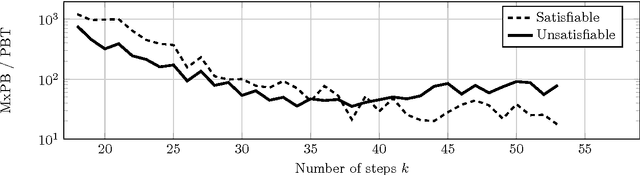
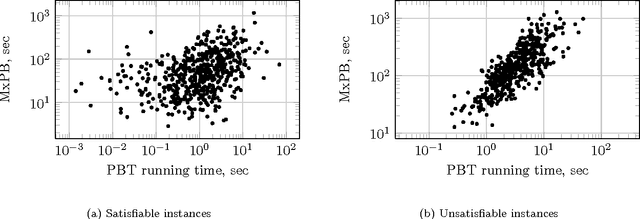
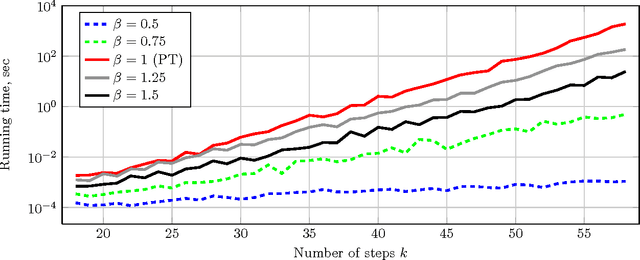
The fixed parameter tractable (FPT) approach is a powerful tool in tackling computationally hard problems. In this paper, we link FPT results to classic artificial intelligence (AI) techniques to show how they complement each other. Specifically, we consider the workflow satisfiability problem (WSP) which asks whether there exists an assignment of authorised users to the steps in a workflow specification, subject to certain constraints on the assignment. It was shown by Cohen et al. (JAIR 2014) that WSP restricted to the class of user-independent constraints (UI), covering many practical cases, admits FPT algorithms, i.e. can be solved in time exponential only in the number of steps $k$ and polynomial in the number of users $n$. Since usually $k \ll n$ in WSP, such FPT algorithms are of great practical interest as they significantly extend the size of the problem that can be routinely solved. We give a new view of the FPT nature of the WSP with UI constraints, showing that it decomposes the problem into two levels. Exploiting this two-level split, we develop a new FPT algorithm that is by many orders of magnitude faster than the previous state-of-the-art WSP algorithm; and it also has only polynomial space complexity whereas the old algorithm takes memory exponential in $k$, which limits its application. We also provide a new pseudo-boolean (PB) formulation of the WSP with UI constraints which exploits this new decomposition of the problem into two levels. Our experiments show that efficiency of solving this new PB formulation of the problem by a general purpose PB solver can be close to the bespoke FPT algorithm, which raises the potential of using general purpose solvers to tackle FPT problems efficiently. We also study the computational performance of various algorithms to complement the overly-pessimistic worst-case analysis that is usually done in FPT studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge