Bi-objective Optimization in Role Mining

Role mining is a technique used to derive a role-based authorization policy from an existing policy. Given a set of users $U$, a set of permissions $P$ and a user-permission authorization relation $\mahtit{UPA}\subseteq U\times P$, a role mining algorithm seeks to compute a set of roles $R$, a user-role authorization relation $\mathit{UA}\subseteq U\times R$ and a permission-role authorization relation $\mathit{PA}\subseteq R\times P$, such that the composition of $\mathit{UA}$ and $\mathit{PA}$ is close (in some appropriate sense) to $\mathit{UPA}$. In this paper, we first introduce the Generalized Noise Role Mining problem (GNRM) -- a generalization of the MinNoise Role Mining problem -- which we believe has considerable practical relevance. Extending work of Fomin et al., we show that GNRM is fixed parameter tractable, with parameter $r + k$, where $r$ is the number of roles in the solution and $k$ is the number of discrepancies between $\mathit{UPA}$ and the relation defined by the composition of $\mathit{UA}$ and $\mathit{PA}$. We further introduce a bi-objective optimization variant of GNRM, where we wish to minimize both $r$ and $k$ subject to upper bounds $r\le \bar{r}$ and $k\le \bar{k}$, where $\bar{r}$ and $\bar{k}$ are constants. We show that the Pareto front of this bi-objective optimization problem (BO-GNRM) can be computed in fixed-parameter tractable time with parameter $\bar{r}+\bar{k}$. We then report the results of our experimental work using the integer programming solver Gurobi to solve instances of BO-GNRM. Our key findings are that (a) we obtained strong support that Gurobi's performance is fixed-parameter tractable, (b) our results suggest that our techniques may be useful for role mining in practice, based on our experiments in the context of three well-known real-world authorization policies.

(1,1)-Cluster Editing is Polynomial-time Solvable

A graph $H$ is a clique graph if $H$ is a vertex-disjoin union of cliques. Abu-Khzam (2017) introduced the $(a,d)$-{Cluster Editing} problem, where for fixed natural numbers $a,d$, given a graph $G$ and vertex-weights $a^*:\ V(G)\rightarrow \{0,1,\dots, a\}$ and $d^*{}:\ V(G)\rightarrow \{0,1,\dots, d\}$, we are to decide whether $G$ can be turned into a cluster graph by deleting at most $d^*(v)$ edges incident to every $v\in V(G)$ and adding at most $a^*(v)$ edges incident to every $v\in V(G)$. Results by Komusiewicz and Uhlmann (2012) and Abu-Khzam (2017) provided a dichotomy of complexity (in P or NP-complete) of $(a,d)$-{Cluster Editing} for all pairs $a,d$ apart from $a=d=1.$ Abu-Khzam (2017) conjectured that $(1,1)$-{Cluster Editing} is in P. We resolve Abu-Khzam's conjecture in affirmative by (i) providing a serious of five polynomial-time reductions to $C_3$-free and $C_4$-free graphs of maximum degree at most 3, and (ii) designing a polynomial-time algorithm for solving $(1,1)$-{Cluster Editing} on $C_3$-free and $C_4$-free graphs of maximum degree at most 3.

Solving the Workflow Satisfiability Problem using General Purpose Solvers

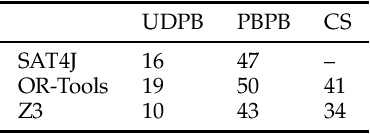
The workflow satisfiability problem (WSP) is a well-studied problem in access control seeking allocation of authorised users to every step of the workflow, subject to workflow specification constraints. It was noticed that the number $k$ of steps is typically small compared to the number of users in the real-world instances of WSP; therefore $k$ is considered as the parameter in WSP parametrised complexity research. While WSP in general was shown to be W[1]-hard, WSP restricted to a special case of user-independent (UI) constraints is fixed-parameter tractable (FPT). However, restriction to the UI constraints might be impractical. To efficiently handle non-UI constraints, we introduce the notion of branching factor of a constraint. As long as the branching factors of the constraints are relatively small and the number of non-UI constraints is reasonable, WSP can be solved in FPT time. Extending the results from Karapetyan et al. (2019), we demonstrate that general-purpose solvers are capable of achieving FPT-like performance on WSP with arbitrary constraints when used with appropriate formulations. This enables one to tackle most of practical WSP instances. While important on its own, we hope that this result will also motivate researchers to look for FPT-aware formulations of other FPT problems.

Pattern-Based Approach to the Workflow Satisfiability Problem with User-Independent Constraints

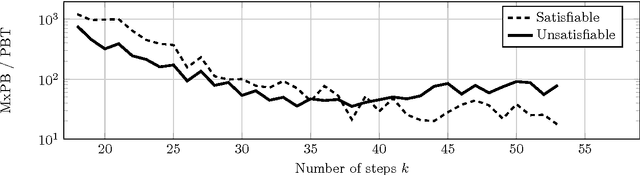
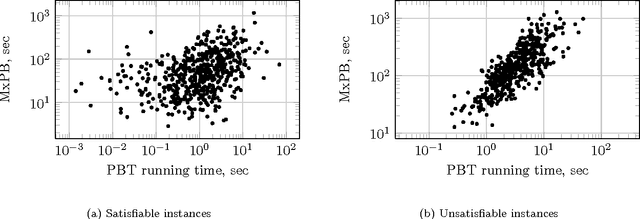
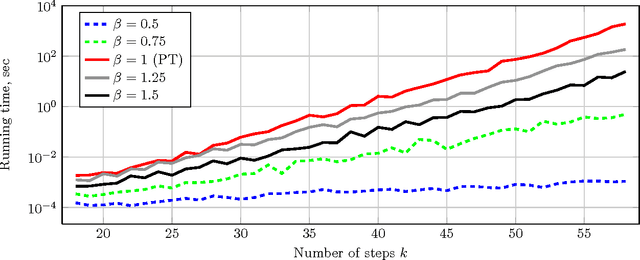
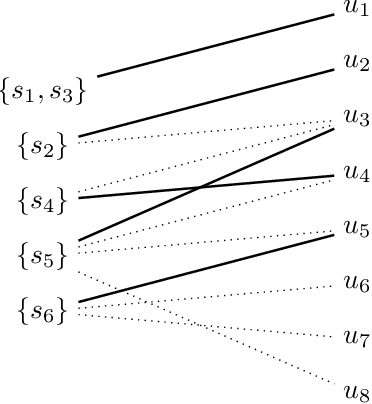
The fixed parameter tractable (FPT) approach is a powerful tool in tackling computationally hard problems. In this paper, we link FPT results to classic artificial intelligence (AI) techniques to show how they complement each other. Specifically, we consider the workflow satisfiability problem (WSP) which asks whether there exists an assignment of authorised users to the steps in a workflow specification, subject to certain constraints on the assignment. It was shown by Cohen et al. (JAIR 2014) that WSP restricted to the class of user-independent constraints (UI), covering many practical cases, admits FPT algorithms, i.e. can be solved in time exponential only in the number of steps $k$ and polynomial in the number of users $n$. Since usually $k \ll n$ in WSP, such FPT algorithms are of great practical interest as they significantly extend the size of the problem that can be routinely solved. We give a new view of the FPT nature of the WSP with UI constraints, showing that it decomposes the problem into two levels. Exploiting this two-level split, we develop a new FPT algorithm that is by many orders of magnitude faster than the previous state-of-the-art WSP algorithm; and it also has only polynomial space complexity whereas the old algorithm takes memory exponential in $k$, which limits its application. We also provide a new pseudo-boolean (PB) formulation of the WSP with UI constraints which exploits this new decomposition of the problem into two levels. Our experiments show that efficiency of solving this new PB formulation of the problem by a general purpose PB solver can be close to the bespoke FPT algorithm, which raises the potential of using general purpose solvers to tackle FPT problems efficiently. We also study the computational performance of various algorithms to complement the overly-pessimistic worst-case analysis that is usually done in FPT studies.