Markov Chain methods for the bipartite Boolean quadratic programming problem
Paper and Code
Oct 24, 2016
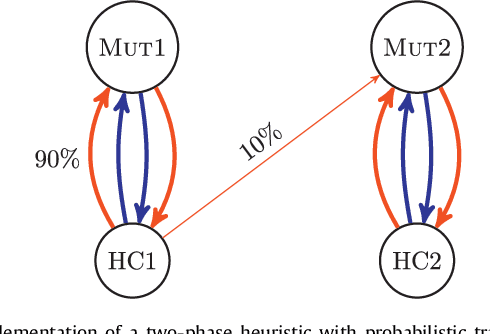
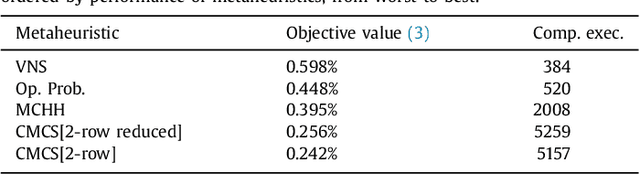
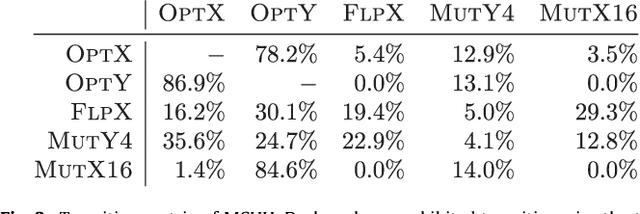
We study the Bipartite Boolean Quadratic Programming Problem (BBQP) which is an extension of the well known Boolean Quadratic Programming Problem (BQP). Applications of the BBQP include mining discrete patterns from binary data, approximating matrices by rank-one binary matrices, computing the cut-norm of a matrix, and solving optimisation problems such as maximum weight biclique, bipartite maximum weight cut, maximum weight induced sub-graph of a bipartite graph, etc. For the BBQP, we first present several algorithmic components, specifically, hill climbers and mutations, and then show how to combine them in a high-performance metaheuristic. Instead of hand-tuning a standard metaheuristic to test the efficiency of the hybrid of the components, we chose to use an automated generation of a multi-component metaheuristic to save human time, and also improve objectivity in the analysis and comparisons of components. For this we designed a new metaheuristic schema which we call Conditional Markov Chain Search (CMCS). We show that CMCS is flexible enough to model several standard metaheuristics; this flexibility is controlled by multiple numeric parameters, and so is convenient for automated generation. We study the configurations revealed by our approach and show that the best of them outperforms the previous state-of-the-art BBQP algorithm by several orders of magnitude. In our experiments we use benchmark instances introduced in the preliminary version of this paper and described here, which have already become the de facto standard in the BBQP literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge