Joint Models for Handling Non-Ignorable Missing Data using Bayesian Additive Regression Trees: Application to Leaf Photosynthetic Traits Data

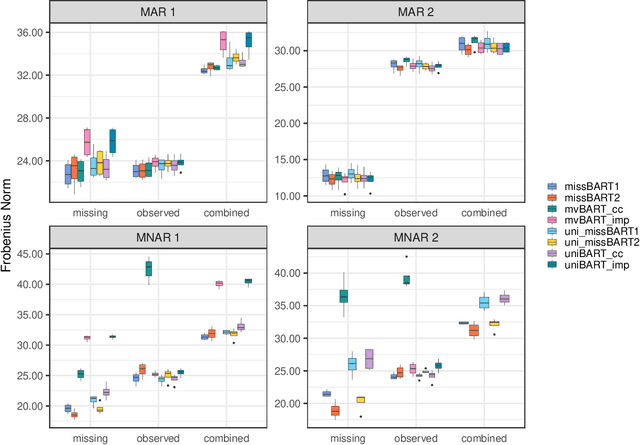
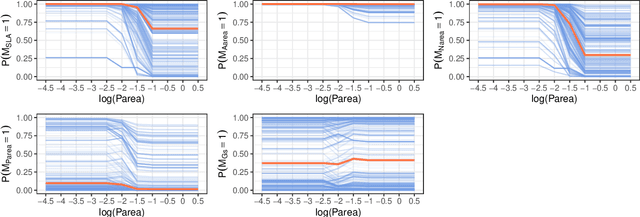
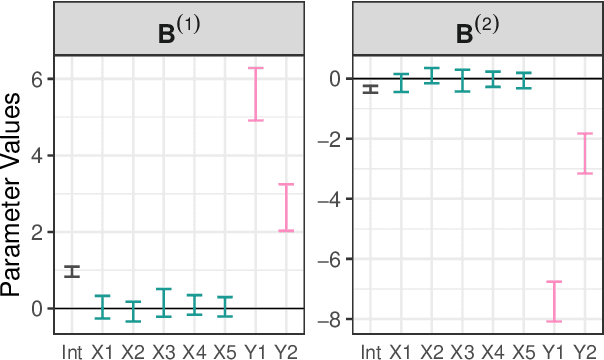
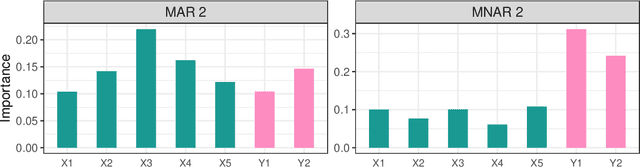
Dealing with missing data poses significant challenges in predictive analysis, often leading to biased conclusions when oversimplified assumptions about the missing data process are made. In cases where the data are missing not at random (MNAR), jointly modeling the data and missing data indicators is essential. Motivated by a real data application with partially missing multivariate outcomes related to leaf photosynthetic traits and several environmental covariates, we propose two methods under a selection model framework for handling data with missingness in the response variables suitable for recovering various missingness mechanisms. Both approaches use a multivariate extension of Bayesian additive regression trees (BART) to flexibly model the outcomes. The first approach simultaneously uses a probit regression model to jointly model the missingness. In scenarios where the relationship between the missingness and the data is more complex or non-linear, we propose a second approach using a probit BART model to characterize the missing data process, thereby employing two BART models simultaneously. Both models also effectively handle ignorable covariate missingness. The efficacy of both models compared to existing missing data approaches is demonstrated through extensive simulations, in both univariate and multivariate settings, and through the aforementioned application to the leaf photosynthetic trait data.

Bayesian Additive Main Effects and Multiplicative Interaction Models using Tensor Regression for Multi-environmental Trials

We propose a Bayesian tensor regression model to accommodate the effect of multiple factors on phenotype prediction. We adopt a set of prior distributions that resolve identifiability issues that may arise between the parameters in the model. Simulation experiments show that our method out-performs previous related models and machine learning algorithms under different sample sizes and degrees of complexity. We further explore the applicability of our model by analysing real-world data related to wheat production across Ireland from 2010 to 2019. Our model performs competitively and overcomes key limitations found in other analogous approaches. Finally, we adapt a set of visualisations for the posterior distribution of the tensor effects that facilitate the identification of optimal interactions between the tensor variables whilst accounting for the uncertainty in the posterior distribution.

Variational Inference for Additive Main and Multiplicative Interaction Effects Models

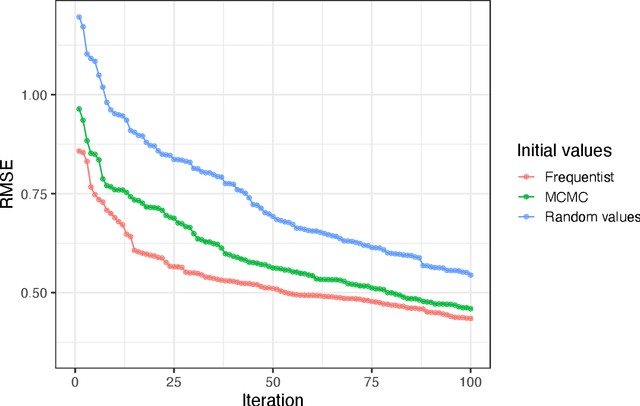
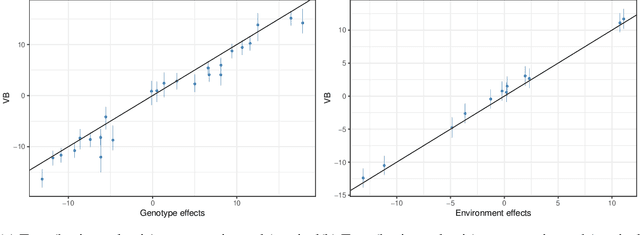
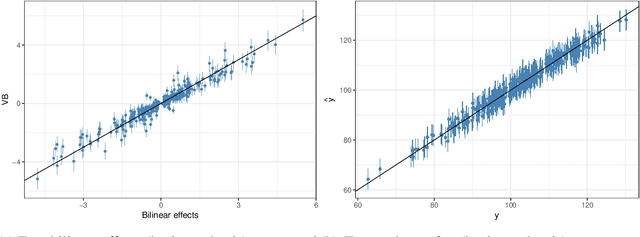
In plant breeding the presence of a genotype by environment (GxE) interaction has a strong impact on cultivation decision making and the introduction of new crop cultivars. The combination of linear and bilinear terms has been shown to be very useful in modelling this type of data. A widely-used approach to identify GxE is the Additive Main Effects and Multiplicative Interaction Effects (AMMI) model. However, as data frequently can be high-dimensional, Markov chain Monte Carlo (MCMC) approaches can be computationally infeasible. In this article, we consider a variational inference approach for such a model. We derive variational approximations for estimating the parameters and we compare the approximations to MCMC using both simulated and real data. The new inferential framework we propose is on average two times faster whilst maintaining the same predictive performance as MCMC.

GP-BART: a novel Bayesian additive regression trees approach using Gaussian processes

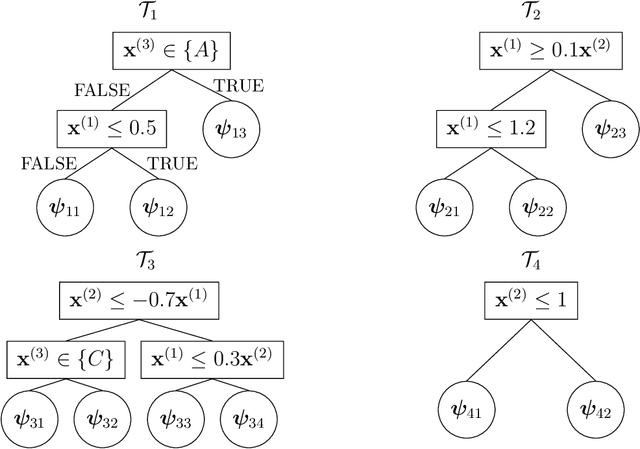
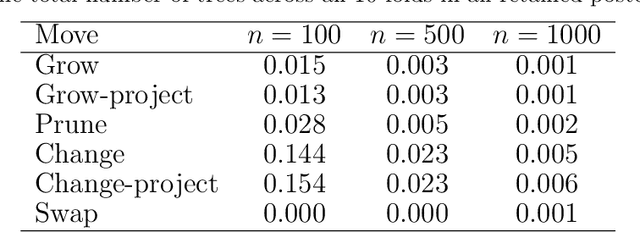
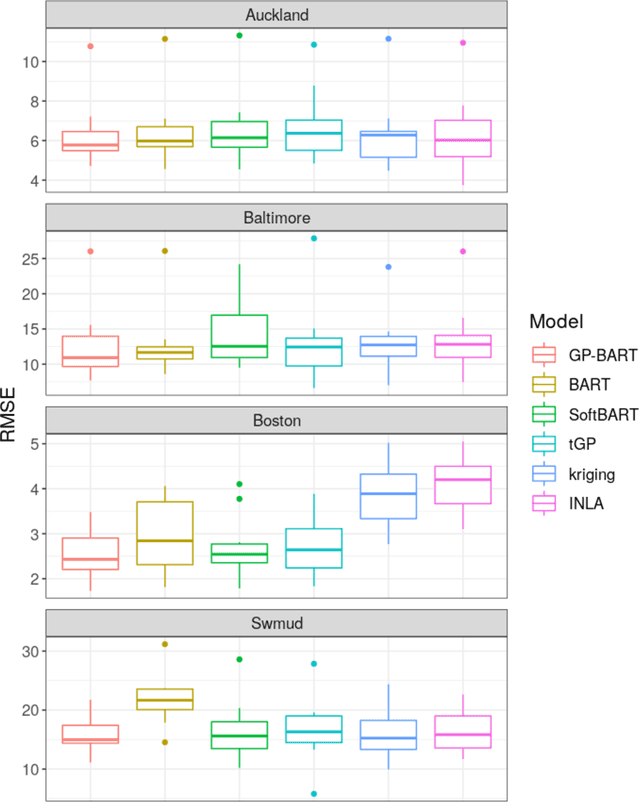
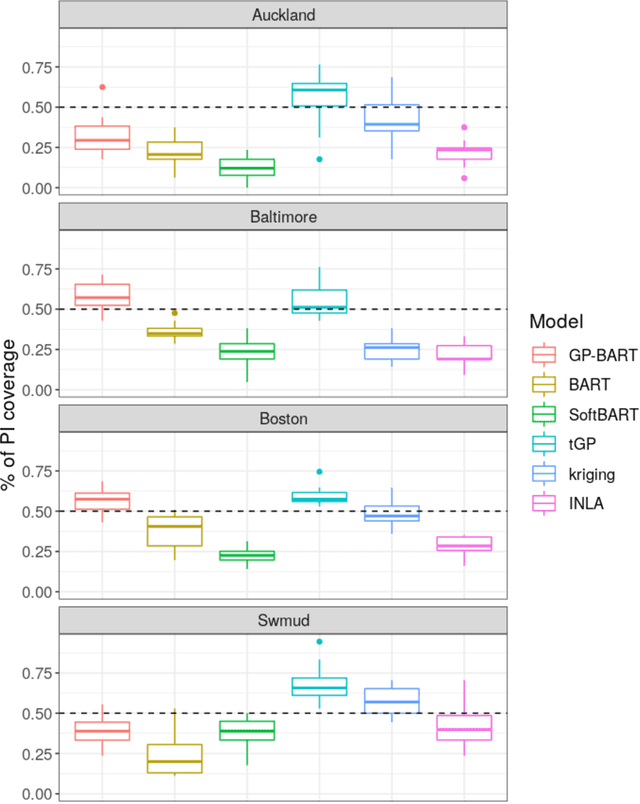
The Bayesian additive regression trees (BART) model is an ensemble method extensively and successfully used in regression tasks due to its consistently strong predictive performance and its ability to quantify uncertainty. BART combines "weak" tree models through a set of shrinkage priors, whereby each tree explains a small portion of the variability in the data. However, the lack of smoothness and the absence of a covariance structure over the observations in standard BART can yield poor performance in cases where such assumptions would be necessary. We propose Gaussian processes Bayesian additive regression trees (GP-BART) as an extension of BART which assumes Gaussian process (GP) priors for the predictions of each terminal node among all trees. We illustrate our model on simulated and real data and compare its performance to traditional modelling approaches, outperforming them in many scenarios. An implementation of our method is available in the R package rGPBART available at: https://github.com/MateusMaiaDS/gpbart

Semi-parametric Bayesian Additive Regression Trees

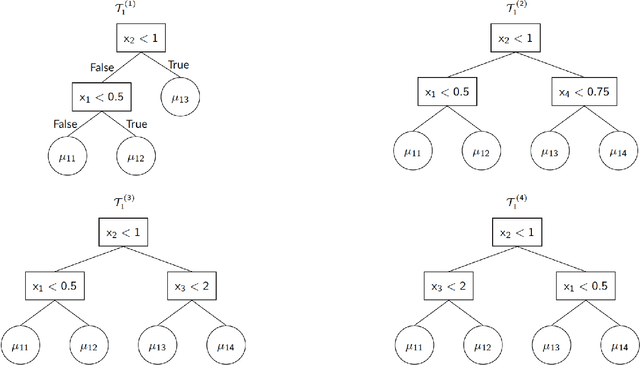
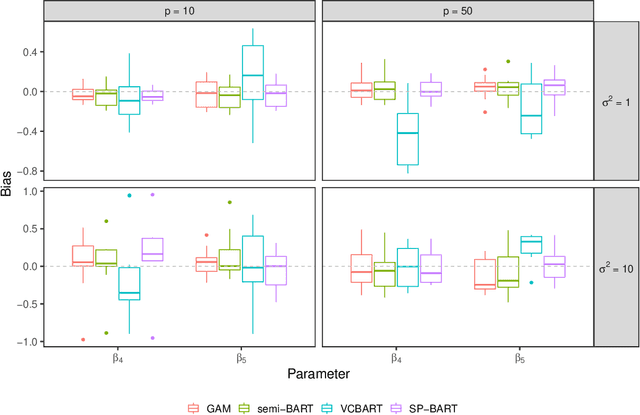
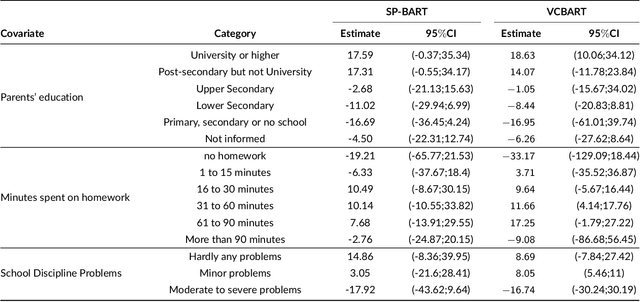
We propose a new semi-parametric model based on Bayesian Additive Regression Trees (BART). In our approach, the response variable is approximated by a linear predictor and a BART model, where the first component is responsible for estimating the main effects and BART accounts for the non-specified interactions and non-linearities. The novelty in our approach lies in the way we change tree generation moves in BART to deal with confounding between the parametric and non-parametric components when they have covariates in common. Through synthetic and real-world examples, we demonstrate that the performance of the new semi-parametric BART is competitive when compared to regression models and other tree-based methods. The implementation of the proposed method is available at https://github.com/ebprado/SP-BART.

Bayesian Additive Regression Trees with Model Trees

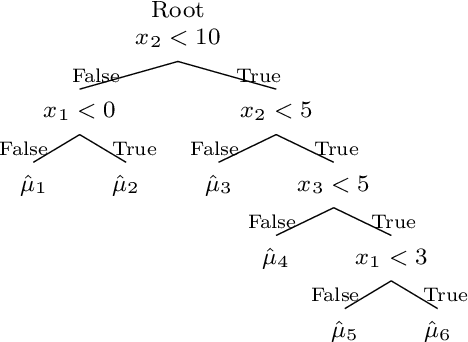
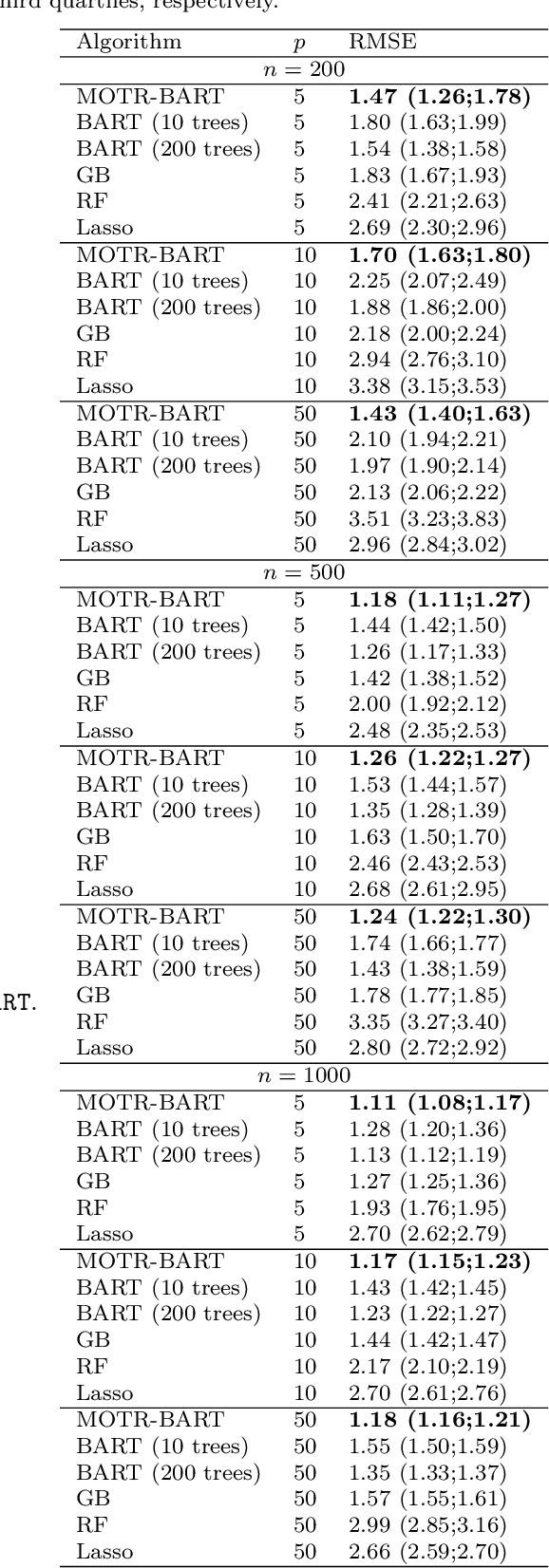
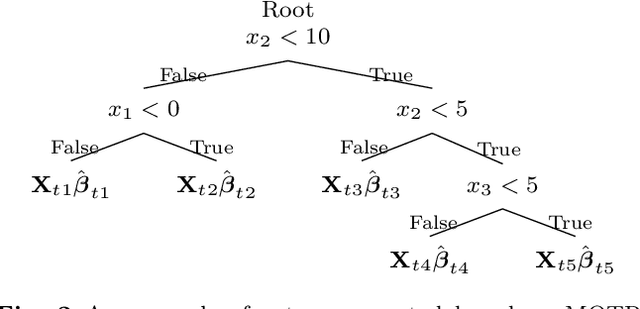
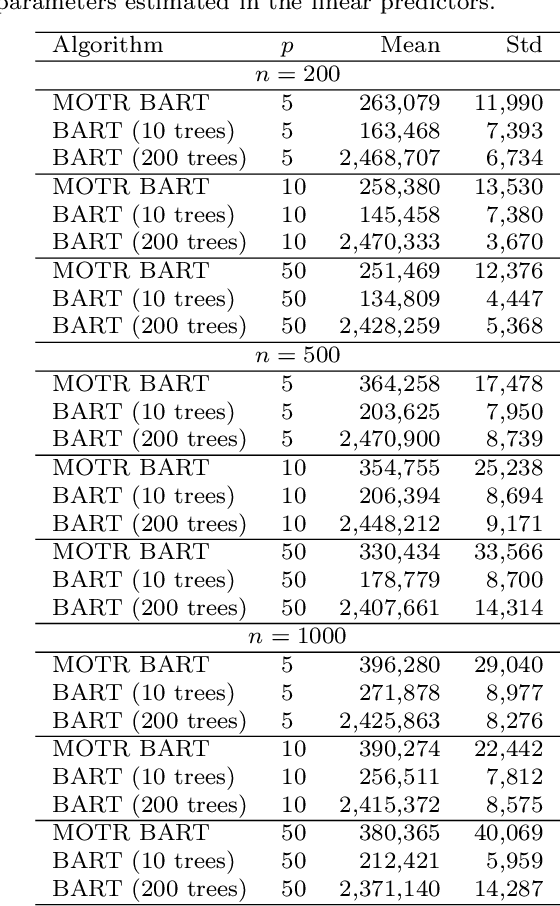
Bayesian Additive Regression Trees (BART) is a tree-based machine learning method that has been successfully applied to regression and classification problems. BART assumes regularisation priors on a set of trees that work as weak learners and is very flexible for predicting in the presence of non-linearity and high-order interactions. In this paper, we introduce an extension of BART, called Model Trees BART (MOTR-BART), that considers piecewise linear functions at node levels instead of piecewise constants. In MOTR-BART, rather than having a unique value at node level for the prediction, a linear predictor is estimated considering the covariates that have been used as the split variables in the corresponding tree. In our approach, local linearities are captured more efficiently and fewer trees are required to achieve equal or better performance than BART. Via simulation studies and real data applications, we compare MOTR-BART to its main competitors. R code for MOTR-BART implementation is available at https://github.com/ebprado/MOTR-BART.