Joint Models for Handling Non-Ignorable Missing Data using Bayesian Additive Regression Trees: Application to Leaf Photosynthetic Traits Data

Dealing with missing data poses significant challenges in predictive analysis, often leading to biased conclusions when oversimplified assumptions about the missing data process are made. In cases where the data are missing not at random (MNAR), jointly modeling the data and missing data indicators is essential. Motivated by a real data application with partially missing multivariate outcomes related to leaf photosynthetic traits and several environmental covariates, we propose two methods under a selection model framework for handling data with missingness in the response variables suitable for recovering various missingness mechanisms. Both approaches use a multivariate extension of Bayesian additive regression trees (BART) to flexibly model the outcomes. The first approach simultaneously uses a probit regression model to jointly model the missingness. In scenarios where the relationship between the missingness and the data is more complex or non-linear, we propose a second approach using a probit BART model to characterize the missing data process, thereby employing two BART models simultaneously. Both models also effectively handle ignorable covariate missingness. The efficacy of both models compared to existing missing data approaches is demonstrated through extensive simulations, in both univariate and multivariate settings, and through the aforementioned application to the leaf photosynthetic trait data.

GP-BART: a novel Bayesian additive regression trees approach using Gaussian processes

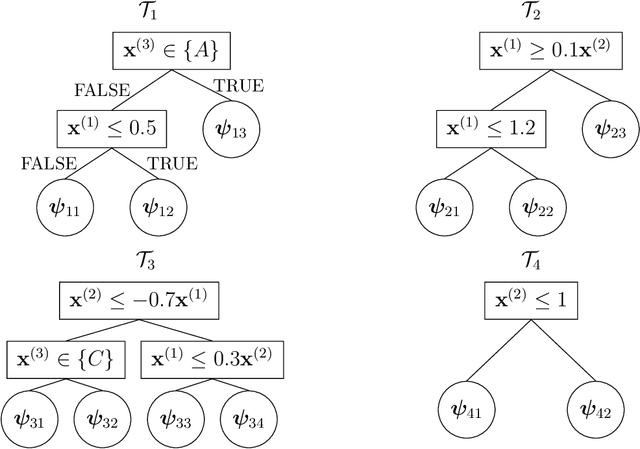
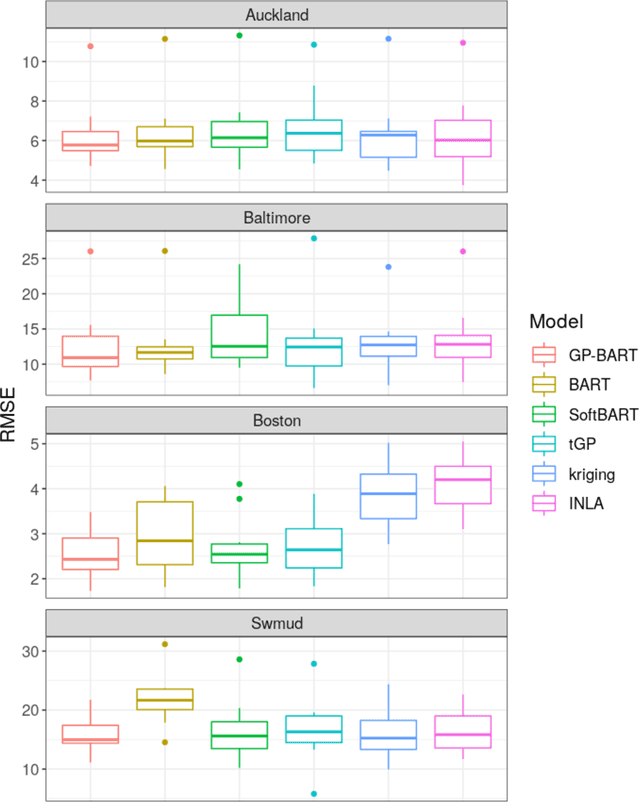
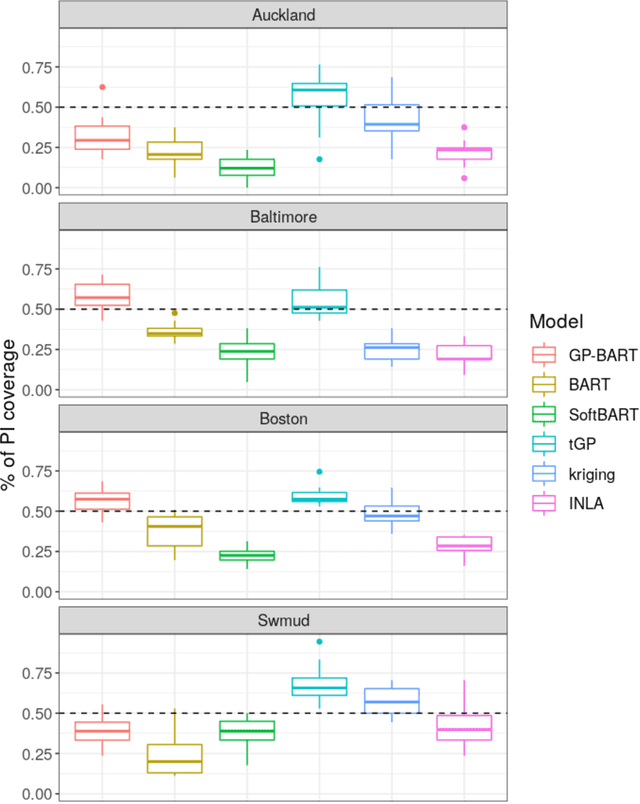
The Bayesian additive regression trees (BART) model is an ensemble method extensively and successfully used in regression tasks due to its consistently strong predictive performance and its ability to quantify uncertainty. BART combines "weak" tree models through a set of shrinkage priors, whereby each tree explains a small portion of the variability in the data. However, the lack of smoothness and the absence of a covariance structure over the observations in standard BART can yield poor performance in cases where such assumptions would be necessary. We propose Gaussian processes Bayesian additive regression trees (GP-BART) as an extension of BART which assumes Gaussian process (GP) priors for the predictions of each terminal node among all trees. We illustrate our model on simulated and real data and compare its performance to traditional modelling approaches, outperforming them in many scenarios. An implementation of our method is available in the R package rGPBART available at: https://github.com/MateusMaiaDS/gpbart