Semi-parametric Bayesian Additive Regression Trees

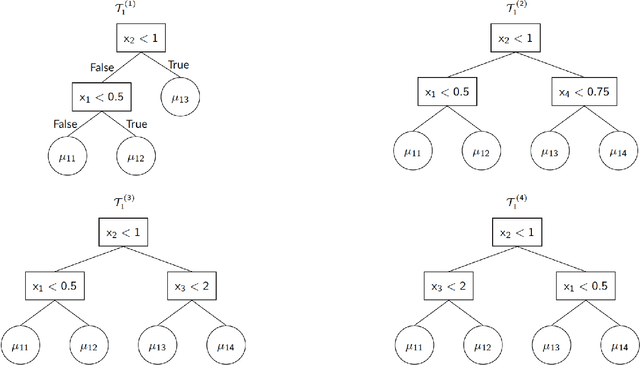
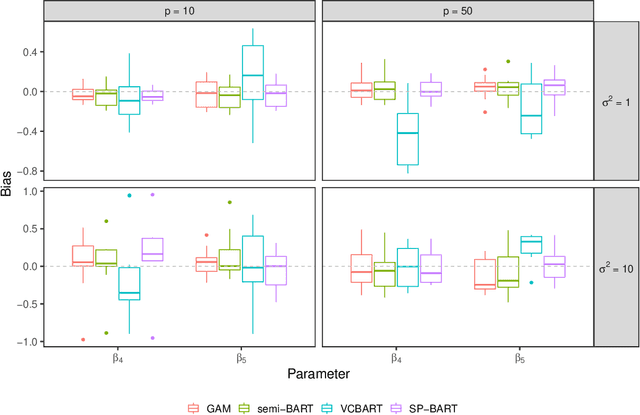
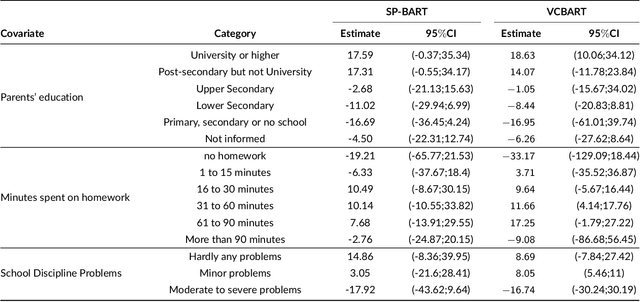
We propose a new semi-parametric model based on Bayesian Additive Regression Trees (BART). In our approach, the response variable is approximated by a linear predictor and a BART model, where the first component is responsible for estimating the main effects and BART accounts for the non-specified interactions and non-linearities. The novelty in our approach lies in the way we change tree generation moves in BART to deal with confounding between the parametric and non-parametric components when they have covariates in common. Through synthetic and real-world examples, we demonstrate that the performance of the new semi-parametric BART is competitive when compared to regression models and other tree-based methods. The implementation of the proposed method is available at https://github.com/ebprado/SP-BART.

Bayesian Additive Regression Trees with Model Trees

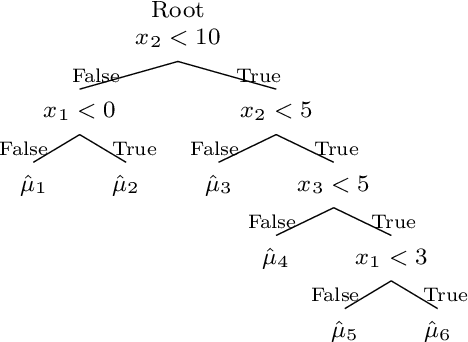
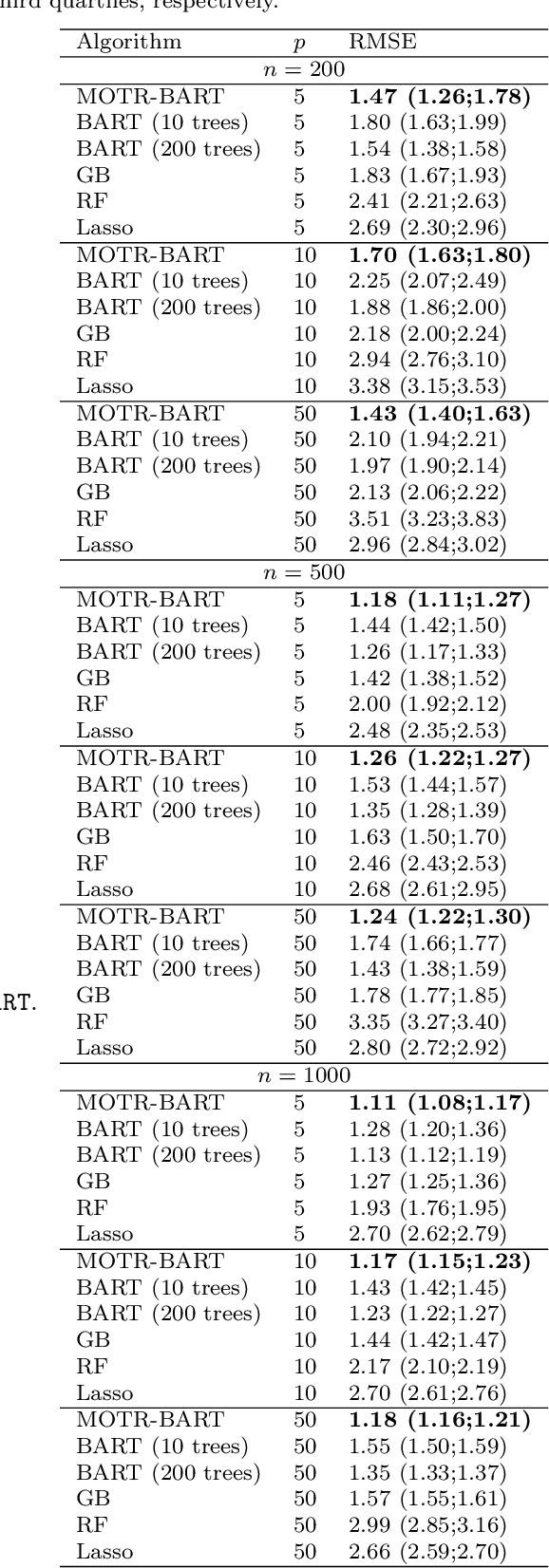
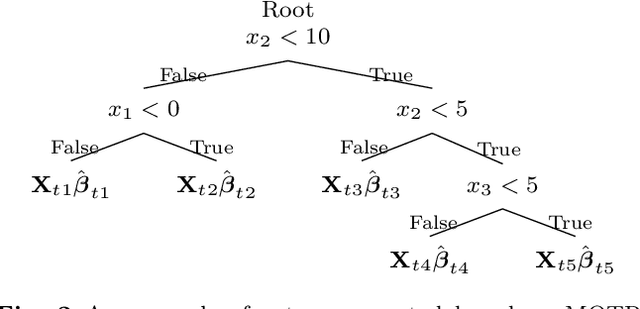
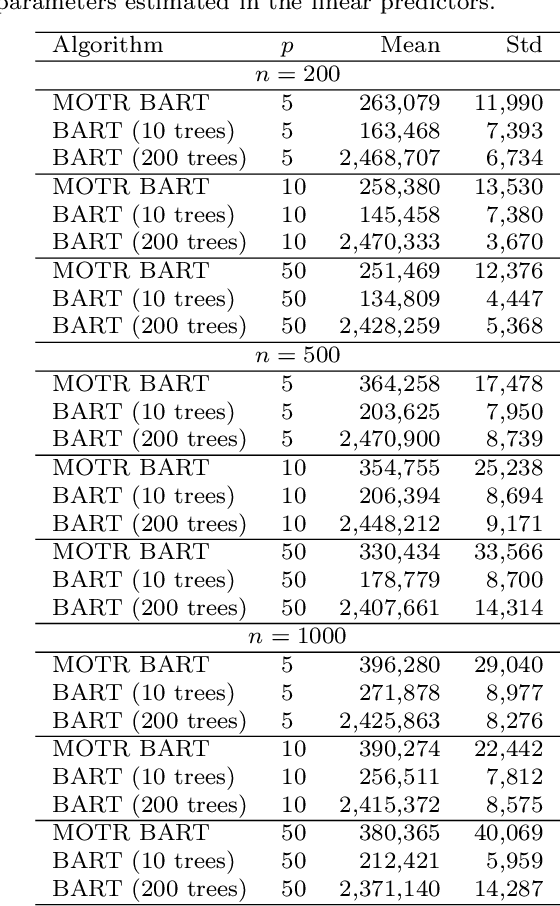
Bayesian Additive Regression Trees (BART) is a tree-based machine learning method that has been successfully applied to regression and classification problems. BART assumes regularisation priors on a set of trees that work as weak learners and is very flexible for predicting in the presence of non-linearity and high-order interactions. In this paper, we introduce an extension of BART, called Model Trees BART (MOTR-BART), that considers piecewise linear functions at node levels instead of piecewise constants. In MOTR-BART, rather than having a unique value at node level for the prediction, a linear predictor is estimated considering the covariates that have been used as the split variables in the corresponding tree. In our approach, local linearities are captured more efficiently and fewer trees are required to achieve equal or better performance than BART. Via simulation studies and real data applications, we compare MOTR-BART to its main competitors. R code for MOTR-BART implementation is available at https://github.com/ebprado/MOTR-BART.