Bayesian Additive Main Effects and Multiplicative Interaction Models using Tensor Regression for Multi-environmental Trials

We propose a Bayesian tensor regression model to accommodate the effect of multiple factors on phenotype prediction. We adopt a set of prior distributions that resolve identifiability issues that may arise between the parameters in the model. Simulation experiments show that our method out-performs previous related models and machine learning algorithms under different sample sizes and degrees of complexity. We further explore the applicability of our model by analysing real-world data related to wheat production across Ireland from 2010 to 2019. Our model performs competitively and overcomes key limitations found in other analogous approaches. Finally, we adapt a set of visualisations for the posterior distribution of the tensor effects that facilitate the identification of optimal interactions between the tensor variables whilst accounting for the uncertainty in the posterior distribution.

Variational Inference for Additive Main and Multiplicative Interaction Effects Models

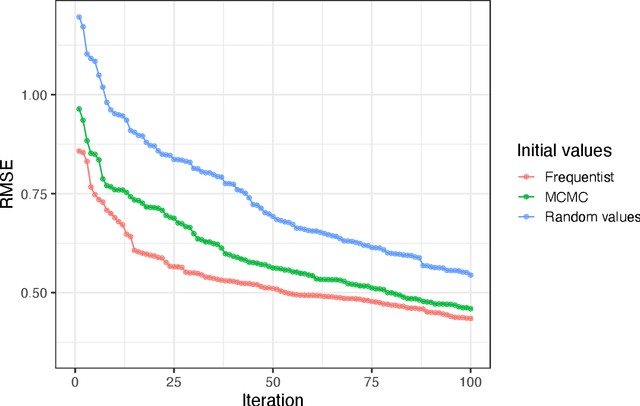
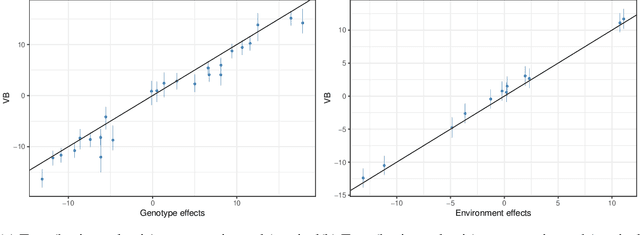
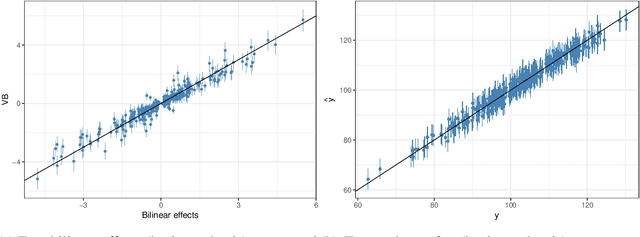
In plant breeding the presence of a genotype by environment (GxE) interaction has a strong impact on cultivation decision making and the introduction of new crop cultivars. The combination of linear and bilinear terms has been shown to be very useful in modelling this type of data. A widely-used approach to identify GxE is the Additive Main Effects and Multiplicative Interaction Effects (AMMI) model. However, as data frequently can be high-dimensional, Markov chain Monte Carlo (MCMC) approaches can be computationally infeasible. In this article, we consider a variational inference approach for such a model. We derive variational approximations for estimating the parameters and we compare the approximations to MCMC using both simulated and real data. The new inferential framework we propose is on average two times faster whilst maintaining the same predictive performance as MCMC.