SCQPTH: an efficient differentiable splitting method for convex quadratic programming

We present SCQPTH: a differentiable first-order splitting method for convex quadratic programs. The SCQPTH framework is based on the alternating direction method of multipliers (ADMM) and the software implementation is motivated by the state-of-the art solver OSQP: an operating splitting solver for convex quadratic programs (QPs). The SCQPTH software is made available as an open-source python package and contains many similar features including efficient reuse of matrix factorizations, infeasibility detection, automatic scaling and parameter selection. The forward pass algorithm performs operator splitting in the dimension of the original problem space and is therefore suitable for large scale QPs with $100-1000$ decision variables and thousands of constraints. Backpropagation is performed by implicit differentiation of the ADMM fixed-point mapping. Experiments demonstrate that for large scale QPs, SCQPTH can provide a $1\times - 10\times$ improvement in computational efficiency in comparison to existing differentiable QP solvers.

Gradient boosting for convex cone predict and optimize problems

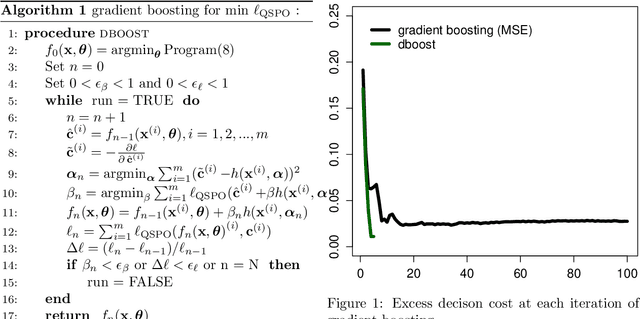
Many problems in engineering and statistics involve both predictive forecasting and decision-based optimization. Traditionally, predictive models are optimized independently from the final decision-based optimization problem. In contrast, a `smart, predict then optimize' (SPO) framework optimizes prediction models to explicitly minimize the final downstream decision loss. In this paper we present dboost, a gradient boosting algorithm for training prediction model ensembles to minimize decision regret. The dboost framework supports any convex optimization program that can be cast as convex quadratic cone program and gradient boosting is performed by implicit differentiation of a custom fixed-point mapping. To our knowledge, the dboost framework is the first general purpose implementation of gradient boosting to predict and optimize problems. Experimental results comparing with state-of-the-art SPO methods show that dboost can further reduce out-of-sample decision regret.

Beyond NaN: Resiliency of Optimization Layers in The Face of Infeasibility

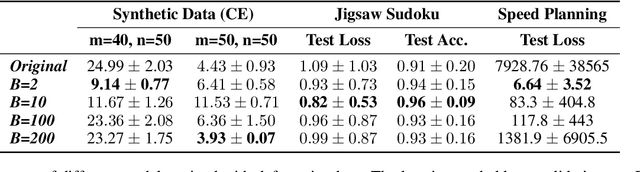
Prior work has successfully incorporated optimization layers as the last layer in neural networks for various problems, thereby allowing joint learning and planning in one neural network forward pass. In this work, we identify a weakness in such a set-up where inputs to the optimization layer lead to undefined output of the neural network. Such undefined decision outputs can lead to possible catastrophic outcomes in critical real time applications. We show that an adversary can cause such failures by forcing rank deficiency on the matrix fed to the optimization layer which results in the optimization failing to produce a solution. We provide a defense for the failure cases by controlling the condition number of the input matrix. We study the problem in the settings of synthetic data, Jigsaw Sudoku, and in speed planning for autonomous driving, building on top of prior frameworks in end-to-end learning and optimization. We show that our proposed defense effectively prevents the framework from failing with undefined output. Finally, we surface a number of edge cases which lead to serious bugs in popular equation and optimization solvers which can be abused as well.

Efficient differentiable quadratic programming layers: an ADMM approach

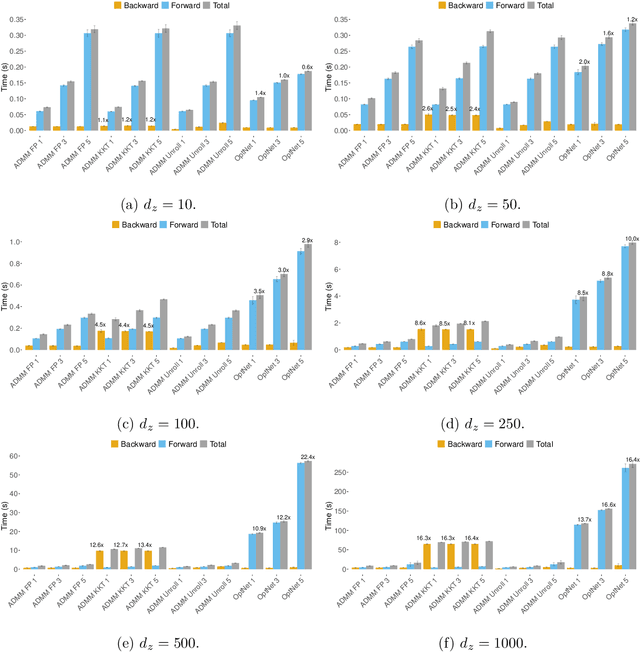
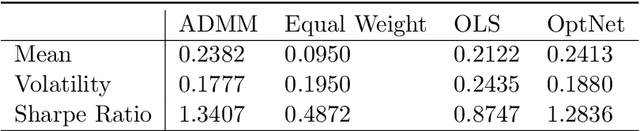
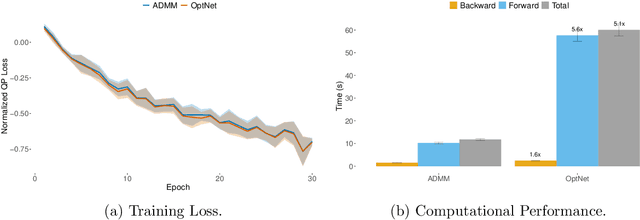
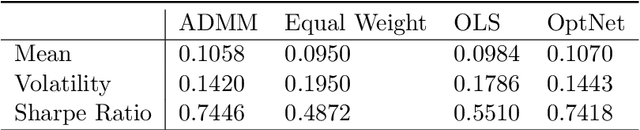
Recent advances in neural-network architecture allow for seamless integration of convex optimization problems as differentiable layers in an end-to-end trainable neural network. Integrating medium and large scale quadratic programs into a deep neural network architecture, however, is challenging as solving quadratic programs exactly by interior-point methods has worst-case cubic complexity in the number of variables. In this paper, we present an alternative network layer architecture based on the alternating direction method of multipliers (ADMM) that is capable of scaling to problems with a moderately large number of variables. Backward differentiation is performed by implicit differentiation of the residual map of a modified fixed-point iteration. Simulated results demonstrate the computational advantage of the ADMM layer, which for medium scaled problems is approximately an order of magnitude faster than the OptNet quadratic programming layer. Furthermore, our novel backward-pass routine is efficient, from both a memory and computation standpoint, in comparison to the standard approach based on unrolled differentiation or implicit differentiation of the KKT optimality conditions. We conclude with examples from portfolio optimization in the integrated prediction and optimization paradigm.