Efficient differentiable quadratic programming layers: an ADMM approach
Paper and Code
Dec 14, 2021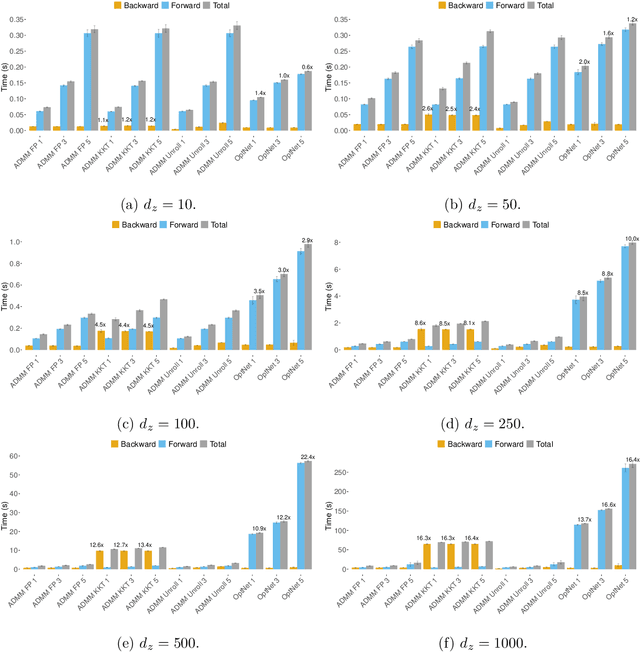
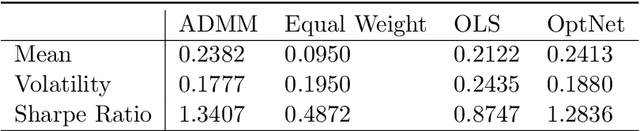
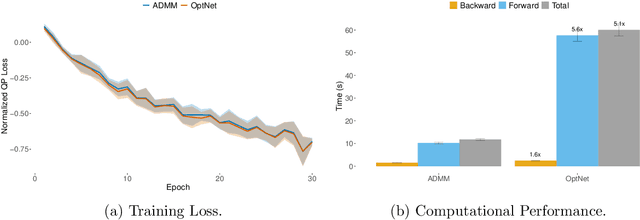
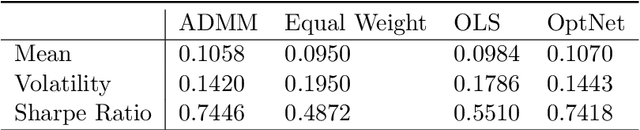
Recent advances in neural-network architecture allow for seamless integration of convex optimization problems as differentiable layers in an end-to-end trainable neural network. Integrating medium and large scale quadratic programs into a deep neural network architecture, however, is challenging as solving quadratic programs exactly by interior-point methods has worst-case cubic complexity in the number of variables. In this paper, we present an alternative network layer architecture based on the alternating direction method of multipliers (ADMM) that is capable of scaling to problems with a moderately large number of variables. Backward differentiation is performed by implicit differentiation of the residual map of a modified fixed-point iteration. Simulated results demonstrate the computational advantage of the ADMM layer, which for medium scaled problems is approximately an order of magnitude faster than the OptNet quadratic programming layer. Furthermore, our novel backward-pass routine is efficient, from both a memory and computation standpoint, in comparison to the standard approach based on unrolled differentiation or implicit differentiation of the KKT optimality conditions. We conclude with examples from portfolio optimization in the integrated prediction and optimization paradigm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge