Computational complexity of Inexact Proximal Point Algorithm for Convex Optimization under Holderian Growth

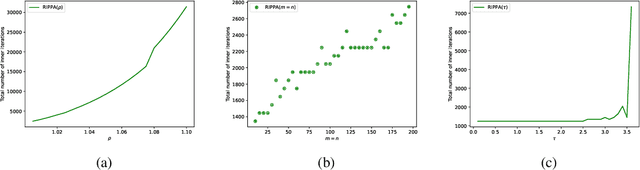
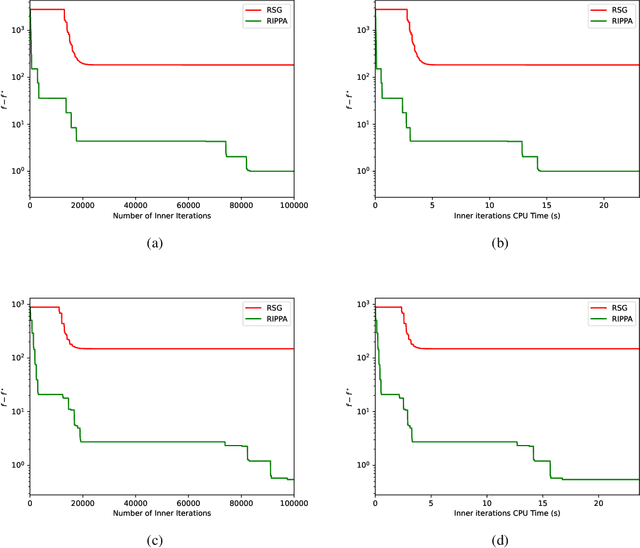
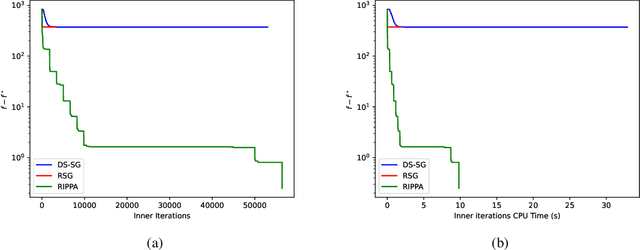
\noindent Several decades ago the Proximal Point Algorithm (PPA) stated to gain a long-lasting attraction for both abstract operator theory and numerical optimization communities. Even in modern applications, researchers still use proximal minimization theory to design scalable algorithms that overcome nonsmoothness. Remarkable works as \cite{Fer:91,Ber:82constrained,Ber:89parallel,Tom:11} established tight relations between the convergence behaviour of PPA and the regularity of the objective function. In this manuscript we derive nonasymptotic iteration complexity of exact and inexact PPA to minimize convex functions under $\gamma-$Holderian growth: $\BigO{\log(1/\epsilon)}$ (for $\gamma \in [1,2]$) and $\BigO{1/\epsilon^{\gamma - 2}}$ (for $\gamma > 2$). In particular, we recover well-known results on PPA: finite convergence for sharp minima and linear convergence for quadratic growth, even under presence of inexactness. However, without taking into account the concrete computational effort paid for computing each PPA iteration, any iteration complexity remains abstract and purely informative. Therefore, using an inner (proximal) gradient/subgradient method subroutine that computes inexact PPA iteration, we secondly show novel computational complexity bounds on a restarted inexact PPA, available when no information on the growth of the objective function is known. In the numerical experiments we confirm the practical performance and implementability of our framework.

Stochastic Proximal Gradient Algorithm with Minibatches. Application to Large Scale Learning Models

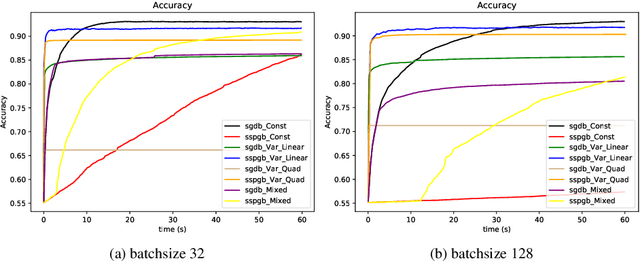
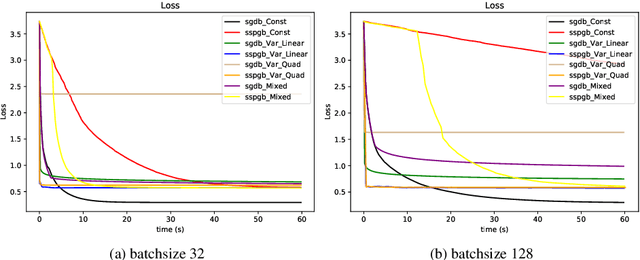
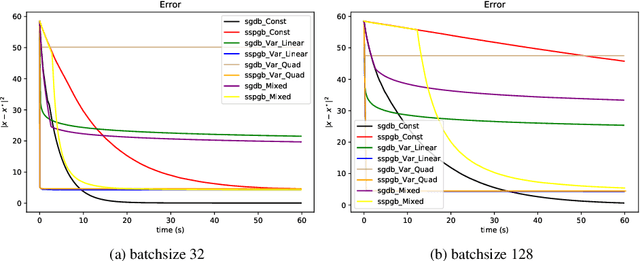
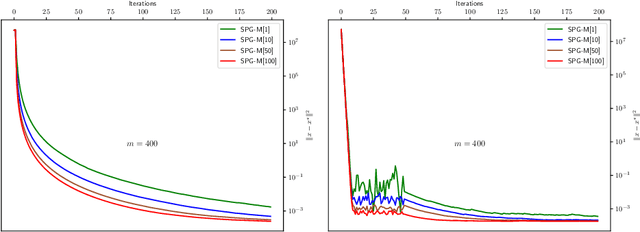
Stochastic optimization lies at the core of most statistical learning models. The recent great development of stochastic algorithmic tools focused significantly onto proximal gradient iterations, in order to find an efficient approach for nonsmooth (composite) population risk functions. The complexity of finding optimal predictors by minimizing regularized risk is largely understood for simple regularizations such as $\ell_1/\ell_2$ norms. However, more complex properties desired for the predictor necessitates highly difficult regularizers as used in grouped lasso or graph trend filtering. In this chapter we develop and analyze minibatch variants of stochastic proximal gradient algorithm for general composite objective functions with stochastic nonsmooth components. We provide iteration complexity for constant and variable stepsize policies obtaining that, for minibatch size $N$, after $\mathcal{O}(\frac{1}{N\epsilon})$ iterations $\epsilon-$suboptimality is attained in expected quadratic distance to optimal solution. The numerical tests on $\ell_2-$regularized SVMs and parametric sparse representation problems confirm the theoretical behaviour and surpasses minibatch SGD performance.

Stochastic proximal splitting algorithm for composite minimization

Supported by the recent contributions in multiple branches, the first-order splitting algorithms became central for structured nonsmooth optimization. In the large-scale or noisy contexts, when only stochastic information on the smooth part of the objective function is available, the extension of proximal gradient schemes to stochastic oracles is based on proximal tractability of the nonsmooth component and it has been deeply analyzed in the literature. However, there remained gaps illustrated by composite models where the nonsmooth term is not proximally tractable anymore. In this note we tackle composite optimization problems, where the access only to stochastic information on both smooth and nonsmooth components is assumed, using a stochastic proximal first-order scheme with stochastic proximal updates. We provide $\mathcal{O}\left( \frac{1}{k} \right)$ the iteration complexity (in expectation of squared distance to the optimal set) under the strong convexity assumption on the objective function. Empirical behavior is illustrated by numerical tests on parametric sparse representation models.

Community-Level Anomaly Detection for Anti-Money Laundering

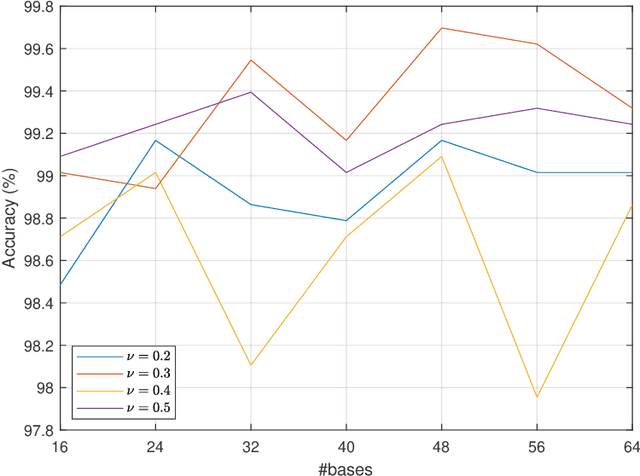
Anomaly detection in networks often boils down to identifying an underlying graph structure on which the abnormal occurrence rests on. Financial fraud schemes are one such example, where more or less intricate schemes are employed in order to elude transaction security protocols. We investigate the problem of learning graph structure representations using adaptations of dictionary learning aimed at encoding connectivity patterns. In particular, we adapt dictionary learning strategies to the specificity of network topologies and propose new methods that impose Laplacian structure on the dictionaries themselves. In one adaption we focus on classifying topologies by working directly on the graph Laplacian and cast the learning problem to accommodate its 2D structure. We tackle the same problem by learning dictionaries which consist of vectorized atomic Laplacians, and provide a block coordinate descent scheme to solve the new dictionary learning formulation. Imposing Laplacian structure on the dictionaries is also proposed in an adaptation of the Single Block Orthogonal learning method. Results on synthetic graph datasets comprising different graph topologies confirm the potential of dictionaries to directly represent graph structure information.

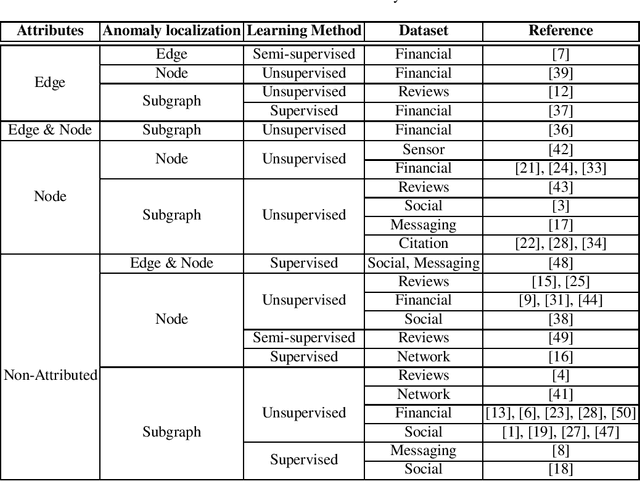
Fraud Detection in Networks: State-of-the-art

Financial fraud detection represents the challenge of finding anomalies in networks of financial transactions. In general, the anomaly detection (AD) is the problem of distinguishing between normal data samples with well defined patterns or signatures and those that do not conform to the expected profiles. The fraudulent behaviour in money laundering may manifest itself through unusual patterns in financial transaction networks. In such networks, nodes represents customers and the edges are transactions: a directed edge between two nodes illustrates that there is a money transfer in the respective direction, where the weight on the edge is the transferred amount. In this paper we present a survey on the fundamental anomaly detection techniques and then present briefly the relevant literature in connection with fraud detection context.

On convergence rate of stochastic proximal point algorithm without strong convexity, smoothness or bounded gradients

Significant parts of the recent learning literature on stochastic optimization algorithms focused on the theoretical and practical behaviour of stochastic first order schemes under different convexity properties. Due to its simplicity, the traditional method of choice for most supervised machine learning problems is the stochastic gradient descent (SGD) method. Many iteration improvements and accelerations have been added to the pure SGD in order to boost its convergence in various (strong) convexity setting. However, the Lipschitz gradient continuity or bounded gradients assumptions are an essential requirement for most existing stochastic first-order schemes. In this paper novel convergence results are presented for the stochastic proximal point algorithm in different settings. In particular, without any strong convexity, smoothness or bounded gradients assumptions, we show that a slightly modified quadratic growth assumption is sufficient to guarantee for the stochastic proximal point $\mathcal{O}\left(\frac{1}{k}\right)$ convergence rate, in terms of the distance to the optimal set. Furthermore, linear convergence is obtained for interpolation setting, when the optimal set of expected cost is included in the optimal sets of each functional component.