Stochastic Proximal Gradient Algorithm with Minibatches. Application to Large Scale Learning Models
Paper and Code
Mar 30, 2020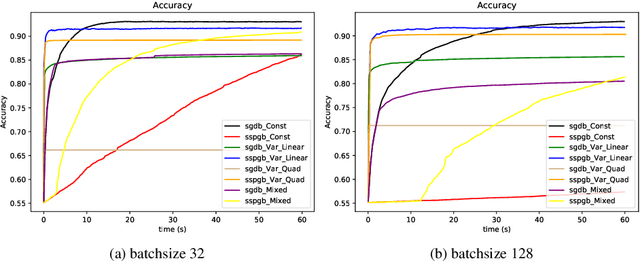
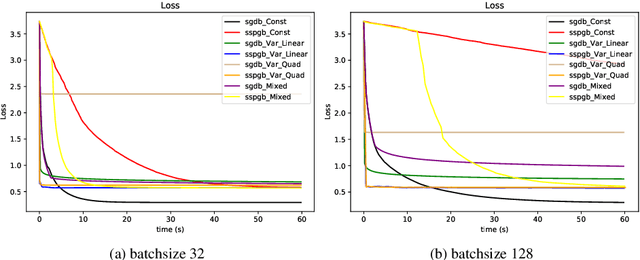
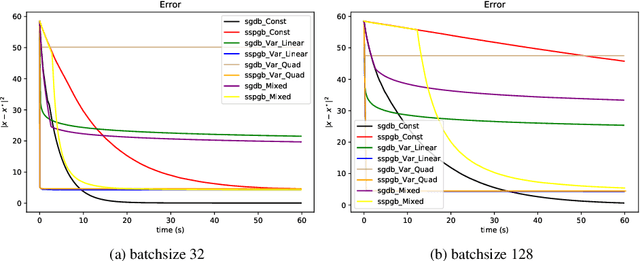
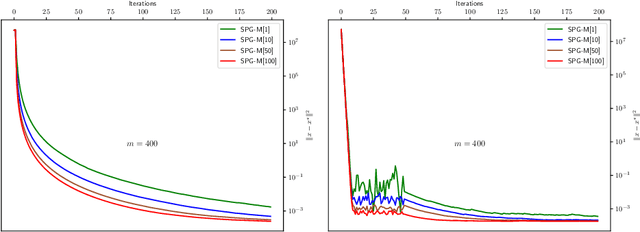
Stochastic optimization lies at the core of most statistical learning models. The recent great development of stochastic algorithmic tools focused significantly onto proximal gradient iterations, in order to find an efficient approach for nonsmooth (composite) population risk functions. The complexity of finding optimal predictors by minimizing regularized risk is largely understood for simple regularizations such as $\ell_1/\ell_2$ norms. However, more complex properties desired for the predictor necessitates highly difficult regularizers as used in grouped lasso or graph trend filtering. In this chapter we develop and analyze minibatch variants of stochastic proximal gradient algorithm for general composite objective functions with stochastic nonsmooth components. We provide iteration complexity for constant and variable stepsize policies obtaining that, for minibatch size $N$, after $\mathcal{O}(\frac{1}{N\epsilon})$ iterations $\epsilon-$suboptimality is attained in expected quadratic distance to optimal solution. The numerical tests on $\ell_2-$regularized SVMs and parametric sparse representation problems confirm the theoretical behaviour and surpasses minibatch SGD performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge