Reinforcement Learning for SBM Graphon Games with Re-Sampling

The Mean-Field approximation is a tractable approach for studying large population dynamics. However, its assumption on homogeneity and universal connections among all agents limits its applicability in many real-world scenarios. Multi-Population Mean-Field Game (MP-MFG) models have been introduced in the literature to address these limitations. When the underlying Stochastic Block Model is known, we show that a Policy Mirror Ascent algorithm finds the MP-MFG Nash Equilibrium. In more realistic scenarios where the block model is unknown, we propose a re-sampling scheme from a graphon integrated with the finite N-player MP-MFG model. We develop a novel learning framework based on a Graphon Game with Re-Sampling (GGR-S) model, which captures the complex network structures of agents' connections. We analyze GGR-S dynamics and establish the convergence to dynamics of MP-MFG. Leveraging this result, we propose an efficient sample-based N-player Reinforcement Learning algorithm for GGR-S without population manipulation, and provide a rigorous convergence analysis with finite sample guarantee.

Provable Fictitious Play for General Mean-Field Games

We propose a reinforcement learning algorithm for stationary mean-field games, where the goal is to learn a pair of mean-field state and stationary policy that constitutes the Nash equilibrium. When viewing the mean-field state and the policy as two players, we propose a fictitious play algorithm which alternatively updates the mean-field state and the policy via gradient-descent and proximal policy optimization, respectively. Our algorithm is in stark contrast with previous literature which solves each single-agent reinforcement learning problem induced by the iterates mean-field states to the optimum. Furthermore, we prove that our fictitious play algorithm converges to the Nash equilibrium at a sublinear rate. To the best of our knowledge, this seems the first provably convergent single-loop reinforcement learning algorithm for mean-field games based on iterative updates of both mean-field state and policy.

Clustering Degree-Corrected Stochastic Block Model with Outliers

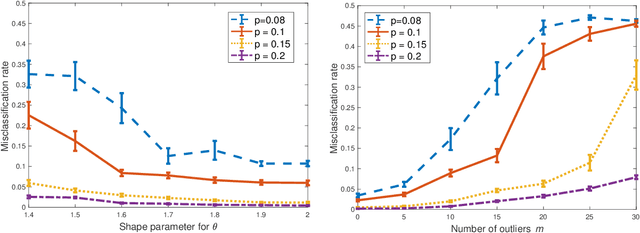
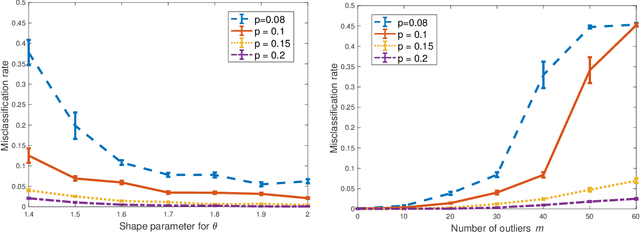
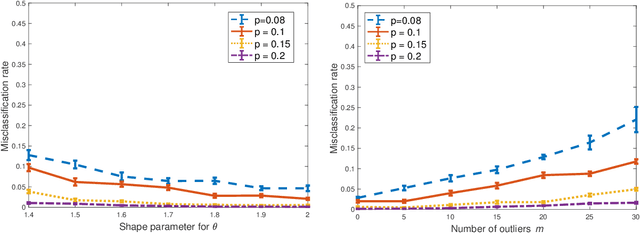
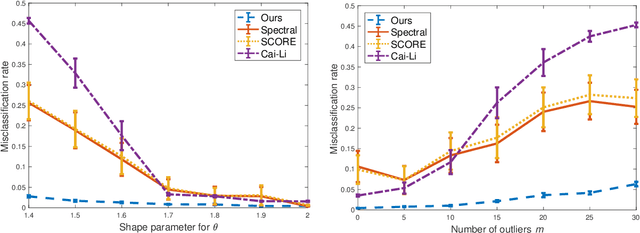
For the degree corrected stochastic block model in the presence of arbitrary or even adversarial outliers, we develop a convex-optimization-based clustering algorithm that includes a penalization term depending on the positive deviation of a node from the expected number of edges to other inliers. We prove that under mild conditions, this method achieves exact recovery of the underlying clusters. Our synthetic experiments show that our algorithm performs well on heterogeneous networks, and in particular those with Pareto degree distributions, for which outliers have a broad range of possible degrees that may enhance their adversarial power. We also demonstrate that our method allows for recovery with significantly lower error rates compared to existing algorithms.