Concentration bounds for linear Monge mapping estimation and optimal transport domain adaptation

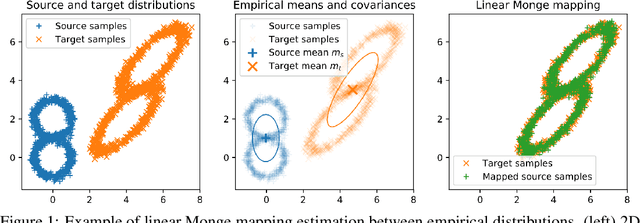
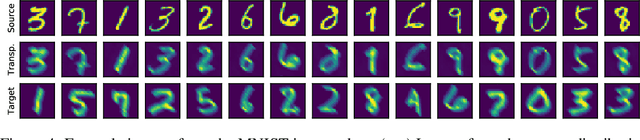
This article investigates the quality of the estimator of the linear Monge mapping between distributions. We provide the first concentration result on the linear mapping operator and prove a sample complexity of $n^{-1/2}$ when using empirical estimates of first and second order moments. This result is then used to derive a generalization bound for domain adaptation with optimal transport. As a consequence, this method approaches the performance of theoretical Bayes predictor under mild conditions on the covariance structure of the problem. We also discuss the computational complexity of the linear mapping estimation and show that when the source and target are stationary the mapping is a convolution that can be estimated very efficiently using fast Fourier transforms. Numerical experiments reproduce the behavior of the proven bounds on simulated and real data for mapping estimation and domain adaptation on images.

Multi-frequency image reconstruction for radio-interferometry with self-tuned regularization parameters

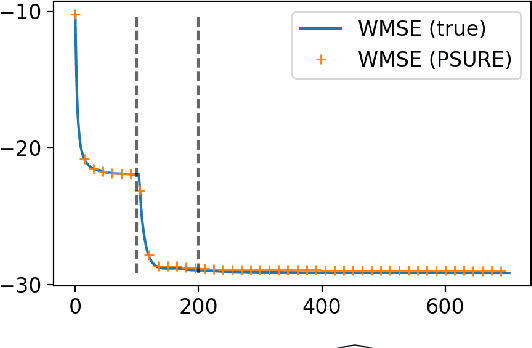
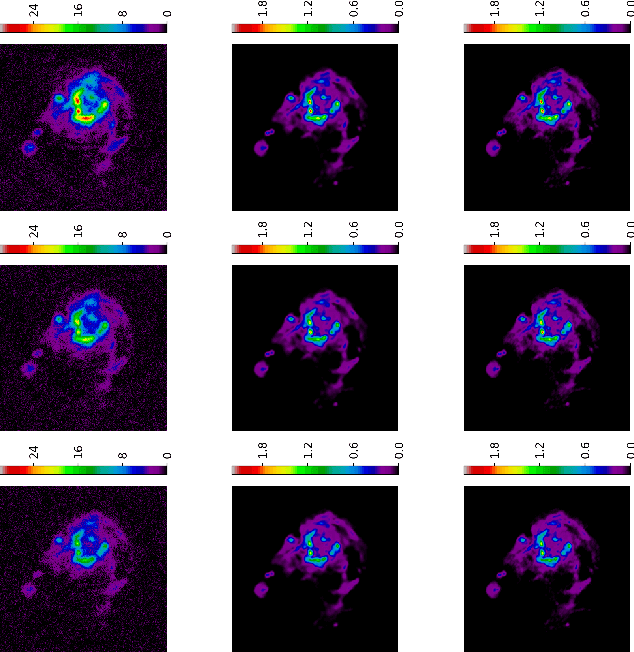
As the world's largest radio telescope, the Square Kilometer Array (SKA) will provide radio interferometric data with unprecedented detail. Image reconstruction algorithms for radio interferometry are challenged to scale well with TeraByte image sizes never seen before. In this work, we investigate one such 3D image reconstruction algorithm known as MUFFIN (MUlti-Frequency image reconstruction For radio INterferometry). In particular, we focus on the challenging task of automatically finding the optimal regularization parameter values. In practice, finding the regularization parameters using classical grid search is computationally intensive and nontrivial due to the lack of ground- truth. We adopt a greedy strategy where, at each iteration, the optimal parameters are found by minimizing the predicted Stein unbiased risk estimate (PSURE). The proposed self-tuned version of MUFFIN involves parallel and computationally efficient steps, and scales well with large- scale data. Finally, numerical results on a 3D image are presented to showcase the performance of the proposed approach.

Distributed image reconstruction for very large arrays in radio astronomy

Current and future radio interferometric arrays such as LOFAR and SKA are characterized by a paradox. Their large number of receptors (up to millions) allow theoretically unprecedented high imaging resolution. In the same time, the ultra massive amounts of samples makes the data transfer and computational loads (correlation and calibration) order of magnitudes too high to allow any currently existing image reconstruction algorithm to achieve, or even approach, the theoretical resolution. We investigate here decentralized and distributed image reconstruction strategies which select, transfer and process only a fraction of the total data. The loss in MSE incurred by the proposed approach is evaluated theoretically and numerically on simple test cases.

A graph Laplacian regularization for hyperspectral data unmixing

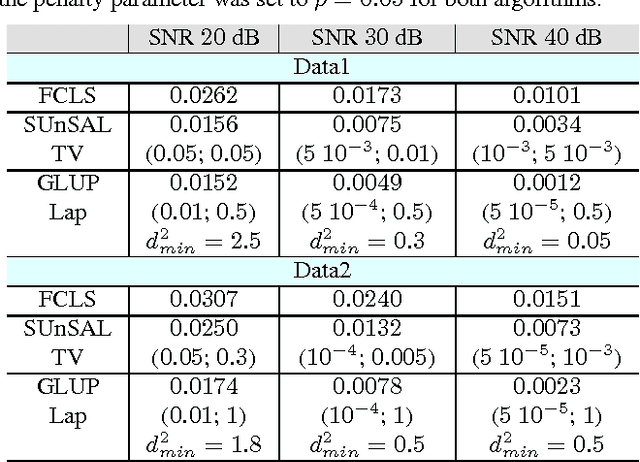
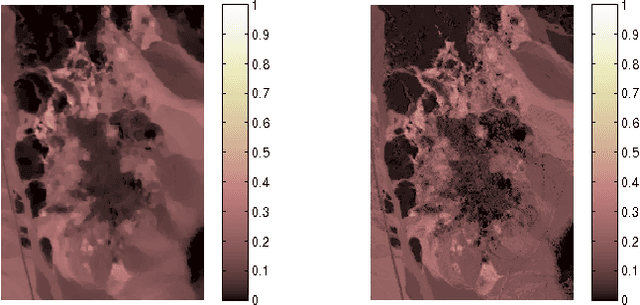
This paper introduces a graph Laplacian regularization in the hyperspectral unmixing formulation. The proposed regularization relies upon the construction of a graph representation of the hyperspectral image. Each node in the graph represents a pixel's spectrum, and edges connect spectrally and spatially similar pixels. The proposed graph framework promotes smoothness in the estimated abundance maps and collaborative estimation between homogeneous areas of the image. The resulting convex optimization problem is solved using the Alternating Direction Method of Multipliers (ADMM). A special attention is given to the computational complexity of the algorithm, and Graph-cut methods are proposed in order to reduce the computational burden. Finally, simulations conducted on synthetic data illustrate the effectiveness of the graph Laplacian regularization with respect to other classical regularizations for hyperspectral unmixing.

PAINTER: a spatio-spectral image reconstruction algorithm for optical interferometry

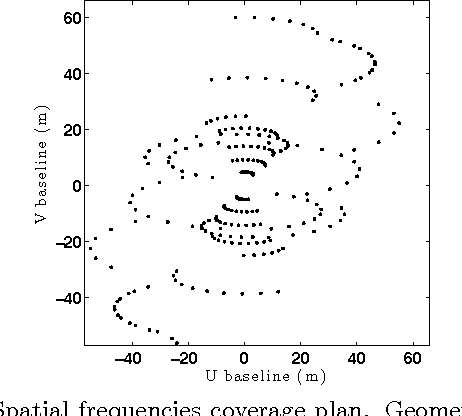
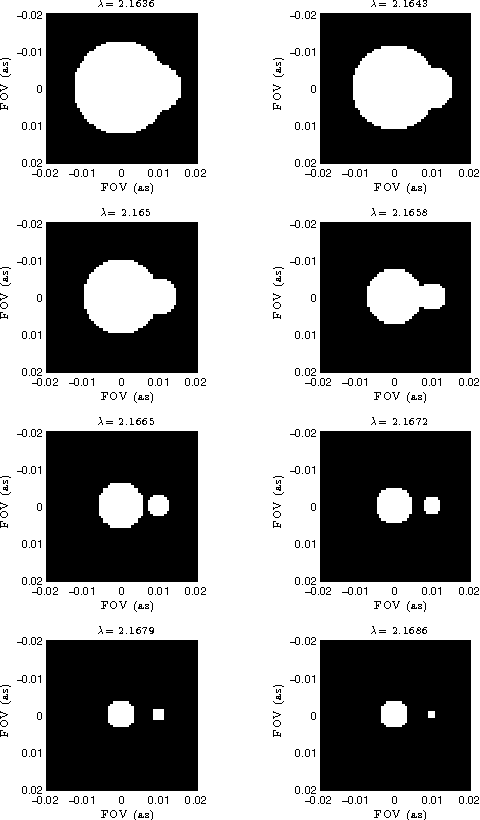
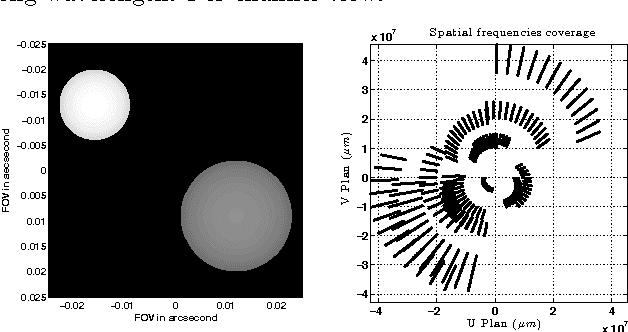
Astronomical optical interferometers sample the Fourier transform of the intensity distribution of a source at the observation wavelength. Because of rapid perturbations caused by atmospheric turbulence, the phases of the complex Fourier samples (visibilities) cannot be directly exploited. Consequently, specific image reconstruction methods have been devised in the last few decades. Modern polychromatic optical interferometric instruments are now paving the way to multiwavelength imaging. This paper is devoted to the derivation of a spatio-spectral (3D) image reconstruction algorithm, coined PAINTER (Polychromatic opticAl INTErferometric Reconstruction software). The algorithm relies on an iterative process, which alternates estimation of polychromatic images and of complex visibilities. The complex visibilities are not only estimated from squared moduli and closure phases, but also differential phases, which helps to better constrain the polychromatic reconstruction. Simulations on synthetic data illustrate the efficiency of the algorithm and in particular the relevance of injecting a differential phases model in the reconstruction.

Blind and fully constrained unmixing of hyperspectral images

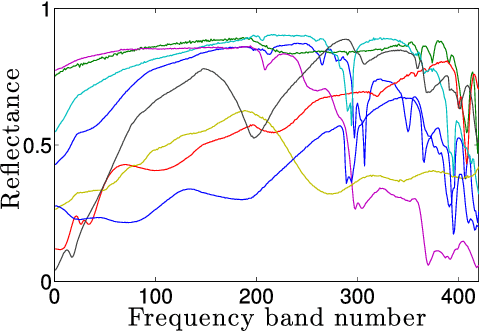
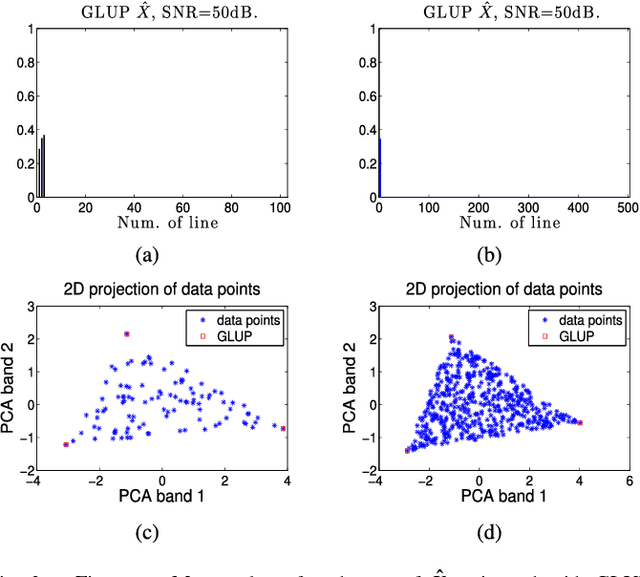
This paper addresses the problem of blind and fully constrained unmixing of hyperspectral images. Unmixing is performed without the use of any dictionary, and assumes that the number of constituent materials in the scene and their spectral signatures are unknown. The estimated abundances satisfy the desired sum-to-one and nonnegativity constraints. Two models with increasing complexity are developed to achieve this challenging task, depending on how noise interacts with hyperspectral data. The first one leads to a convex optimization problem, and is solved with the Alternating Direction Method of Multipliers. The second one accounts for signal-dependent noise, and is addressed with a Reweighted Least Squares algorithm. Experiments on synthetic and real data demonstrate the effectiveness of our approach.