A graph Laplacian regularization for hyperspectral data unmixing
Paper and Code
Oct 14, 2014
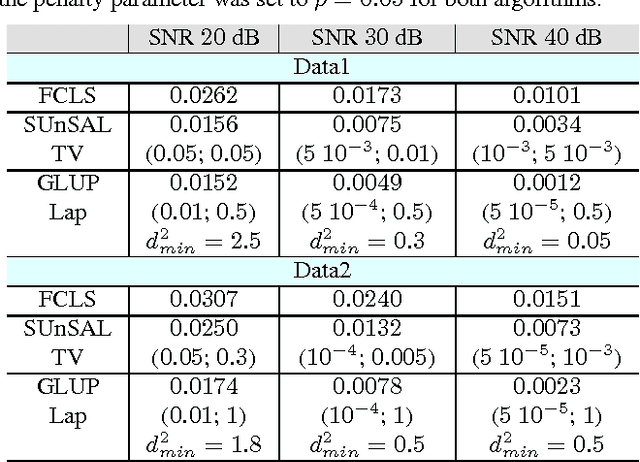
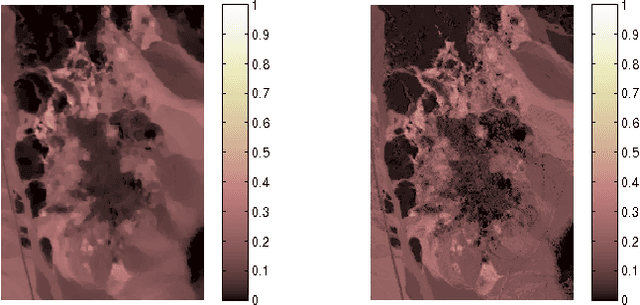
This paper introduces a graph Laplacian regularization in the hyperspectral unmixing formulation. The proposed regularization relies upon the construction of a graph representation of the hyperspectral image. Each node in the graph represents a pixel's spectrum, and edges connect spectrally and spatially similar pixels. The proposed graph framework promotes smoothness in the estimated abundance maps and collaborative estimation between homogeneous areas of the image. The resulting convex optimization problem is solved using the Alternating Direction Method of Multipliers (ADMM). A special attention is given to the computational complexity of the algorithm, and Graph-cut methods are proposed in order to reduce the computational burden. Finally, simulations conducted on synthetic data illustrate the effectiveness of the graph Laplacian regularization with respect to other classical regularizations for hyperspectral unmixing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge