Multi-frequency image reconstruction for radio-interferometry with self-tuned regularization parameters

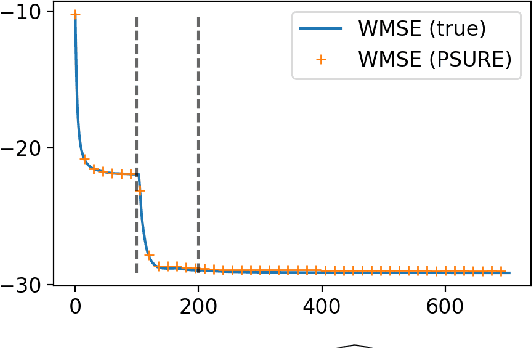
As the world's largest radio telescope, the Square Kilometer Array (SKA) will provide radio interferometric data with unprecedented detail. Image reconstruction algorithms for radio interferometry are challenged to scale well with TeraByte image sizes never seen before. In this work, we investigate one such 3D image reconstruction algorithm known as MUFFIN (MUlti-Frequency image reconstruction For radio INterferometry). In particular, we focus on the challenging task of automatically finding the optimal regularization parameter values. In practice, finding the regularization parameters using classical grid search is computationally intensive and nontrivial due to the lack of ground- truth. We adopt a greedy strategy where, at each iteration, the optimal parameters are found by minimizing the predicted Stein unbiased risk estimate (PSURE). The proposed self-tuned version of MUFFIN involves parallel and computationally efficient steps, and scales well with large- scale data. Finally, numerical results on a 3D image are presented to showcase the performance of the proposed approach.

A graph Laplacian regularization for hyperspectral data unmixing

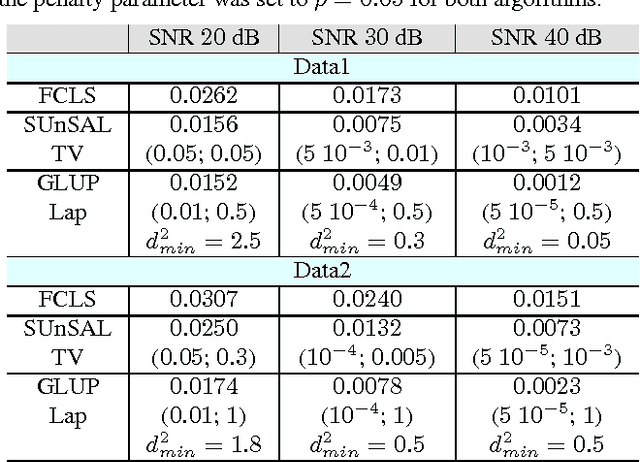
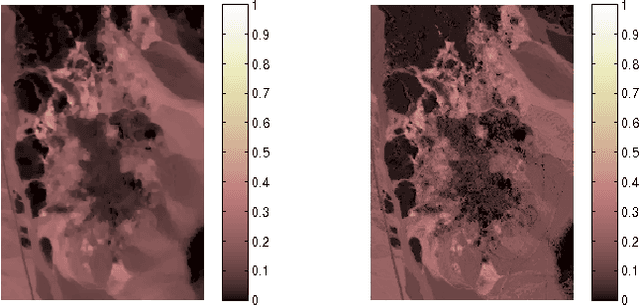
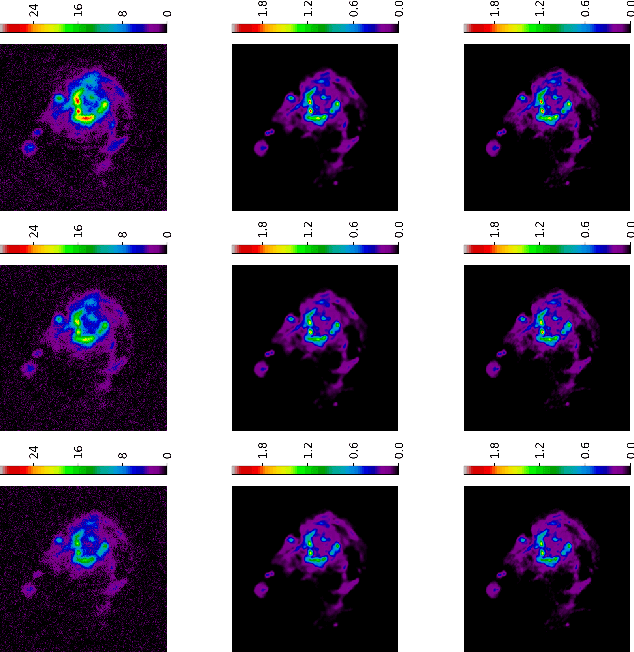
This paper introduces a graph Laplacian regularization in the hyperspectral unmixing formulation. The proposed regularization relies upon the construction of a graph representation of the hyperspectral image. Each node in the graph represents a pixel's spectrum, and edges connect spectrally and spatially similar pixels. The proposed graph framework promotes smoothness in the estimated abundance maps and collaborative estimation between homogeneous areas of the image. The resulting convex optimization problem is solved using the Alternating Direction Method of Multipliers (ADMM). A special attention is given to the computational complexity of the algorithm, and Graph-cut methods are proposed in order to reduce the computational burden. Finally, simulations conducted on synthetic data illustrate the effectiveness of the graph Laplacian regularization with respect to other classical regularizations for hyperspectral unmixing.

Blind and fully constrained unmixing of hyperspectral images

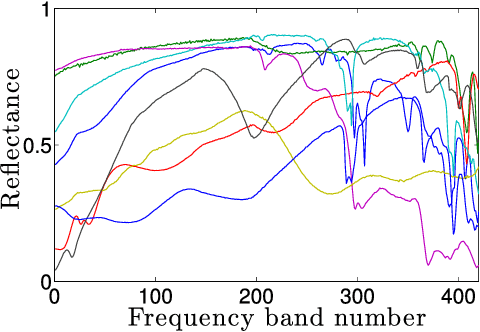
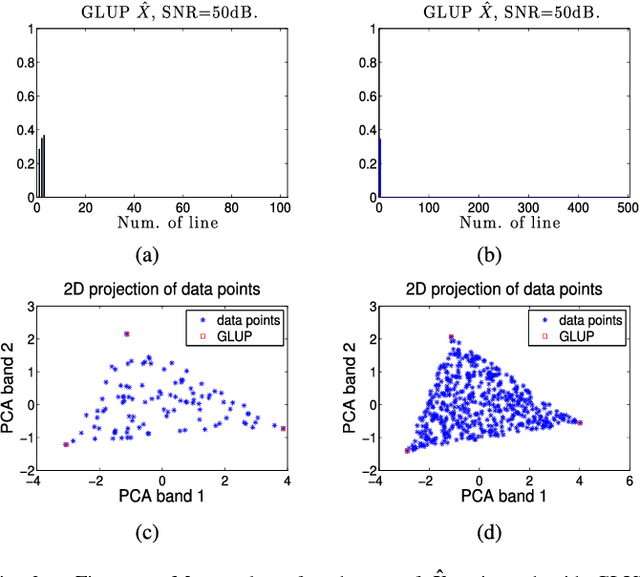
This paper addresses the problem of blind and fully constrained unmixing of hyperspectral images. Unmixing is performed without the use of any dictionary, and assumes that the number of constituent materials in the scene and their spectral signatures are unknown. The estimated abundances satisfy the desired sum-to-one and nonnegativity constraints. Two models with increasing complexity are developed to achieve this challenging task, depending on how noise interacts with hyperspectral data. The first one leads to a convex optimization problem, and is solved with the Alternating Direction Method of Multipliers. The second one accounts for signal-dependent noise, and is addressed with a Reweighted Least Squares algorithm. Experiments on synthetic and real data demonstrate the effectiveness of our approach.