Nonasymptotic Regret Analysis of Adaptive Linear Quadratic Control with Model Misspecification

The strategy of pre-training a large model on a diverse dataset, then fine-tuning for a particular application has yielded impressive results in computer vision, natural language processing, and robotic control. This strategy has vast potential in adaptive control, where it is necessary to rapidly adapt to changing conditions with limited data. Toward concretely understanding the benefit of pre-training for adaptive control, we study the adaptive linear quadratic control problem in the setting where the learner has prior knowledge of a collection of basis matrices for the dynamics. This basis is misspecified in the sense that it cannot perfectly represent the dynamics of the underlying data generating process. We propose an algorithm that uses this prior knowledge, and prove upper bounds on the expected regret after $T$ interactions with the system. In the regime where $T$ is small, the upper bounds are dominated by a term scales with either $\texttt{poly}(\log T)$ or $\sqrt{T}$, depending on the prior knowledge available to the learner. When $T$ is large, the regret is dominated by a term that grows with $\delta T$, where $\delta$ quantifies the level of misspecification. This linear term arises due to the inability to perfectly estimate the underlying dynamics using the misspecified basis, and is therefore unavoidable unless the basis matrices are also adapted online. However, it only dominates for large $T$, after the sublinear terms arising due to the error in estimating the weights for the basis matrices become negligible. We provide simulations that validate our analysis. Our simulations also show that offline data from a collection of related systems can be used as part of a pre-training stage to estimate a misspecified dynamics basis, which is in turn used by our adaptive controller.

From self-tuning regulators to reinforcement learning and back again

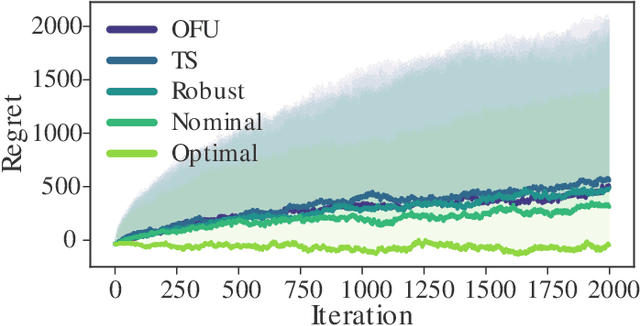
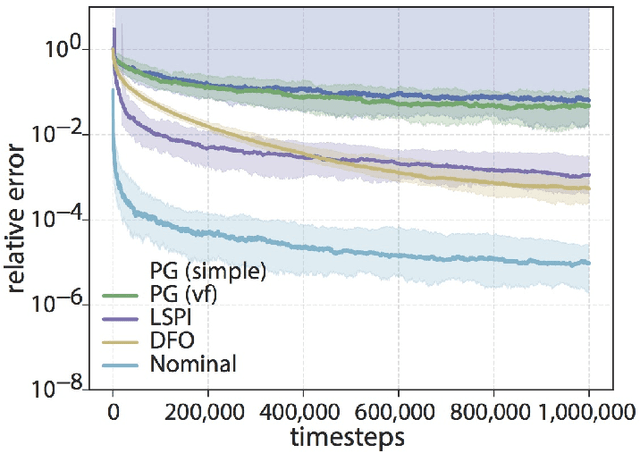
Machine and reinforcement learning (RL) are being applied to plan and control the behavior of autonomous systems interacting with the physical world -- examples include self-driving vehicles, distributed sensor networks, and agile robots. However, if machine learning is to be applied in these new settings, the resulting algorithms must come with the reliability, robustness, and safety guarantees that are hallmarks of the control theory literature, as failures could be catastrophic. Thus, as RL algorithms are increasingly and more aggressively deployed in safety critical settings, it is imperative that control theorists be part of the conversation. The goal of this tutorial paper is to provide a jumping off point for control theorists wishing to work on RL related problems by covering recent advances in bridging learning and control theory, and by placing these results within the appropriate historical context of the system identification and adaptive control literatures.

Low-rank Optimization with Convex Constraints

The problem of low-rank approximation with convex constraints, which appears in data analysis, system identification, model order reduction, low-order controller design and low-complexity modelling is considered. Given a matrix, the objective is to find a low-rank approximation that meets rank and convex constraints, while minimizing the distance to the matrix in the squared Frobenius norm. In many situations, this non-convex problem is convexified by nuclear norm regularization. However, we will see that the approximations obtained by this method may be far from optimal. In this paper, we propose an alternative convex relaxation that uses the convex envelope of the squared Frobenius norm and the rank constraint. With this approach, easily verifiable conditions are obtained under which the solutions to the convex relaxation and the original non-convex problem coincide. An SDP representation of the convex envelope is derived, which allows us to apply this approach to several known problems. Our example on optimal low-rank Hankel approximation/model reduction illustrates that the proposed convex relaxation performs consistently better than nuclear norm regularization and may outperform balanced truncation.

A Unified Analysis of Stochastic Optimization Methods Using Jump System Theory and Quadratic Constraints

We develop a simple routine unifying the analysis of several important recently-developed stochastic optimization methods including SAGA, Finito, and stochastic dual coordinate ascent (SDCA). First, we show an intrinsic connection between stochastic optimization methods and dynamic jump systems, and propose a general jump system model for stochastic optimization methods. Our proposed model recovers SAGA, SDCA, Finito, and SAG as special cases. Then we combine jump system theory with several simple quadratic inequalities to derive sufficient conditions for convergence rate certifications of the proposed jump system model under various assumptions (with or without individual convexity, etc). The derived conditions are linear matrix inequalities (LMIs) whose sizes roughly scale with the size of the training set. We make use of the symmetry in the stochastic optimization methods and reduce these LMIs to some equivalent small LMIs whose sizes are at most 3 by 3. We solve these small LMIs to provide analytical proofs of new convergence rates for SAGA, Finito and SDCA (with or without individual convexity). We also explain why our proposed LMI fails in analyzing SAG. We reveal a key difference between SAG and other methods, and briefly discuss how to extend our LMI analysis for SAG. An advantage of our approach is that the proposed analysis can be automated for a large class of stochastic methods under various assumptions (with or without individual convexity, etc).