The Penalty Imposed by Ablated Data Augmentation

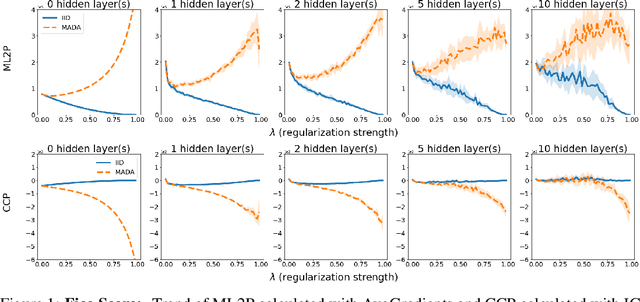
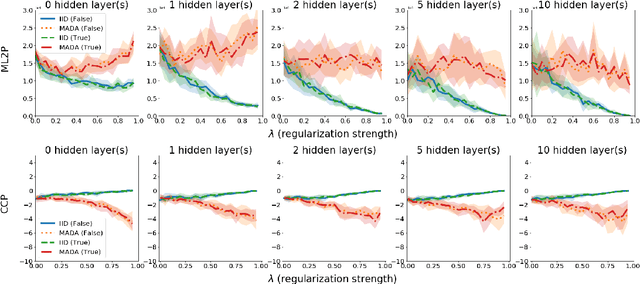
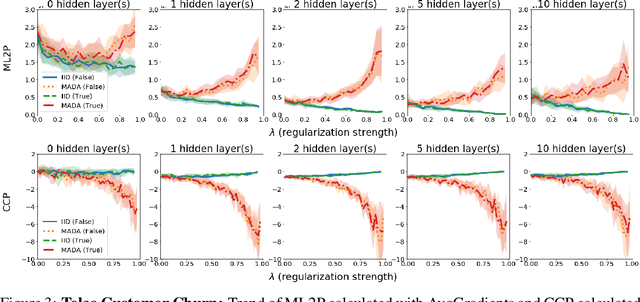
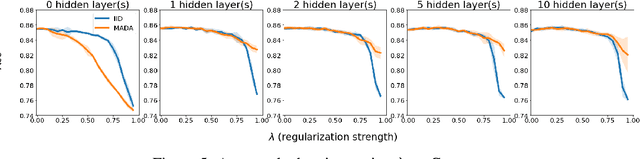
There is a set of data augmentation techniques that ablate parts of the input at random. These include input dropout, cutout, and random erasing. We term these techniques ablated data augmentation. Though these techniques seems similar in spirit and have shown success in improving model performance in a variety of domains, we do not yet have a mathematical understanding of the differences between these techniques like we do for other regularization techniques like L1 or L2. First, we study a formal model of mean ablated data augmentation and inverted dropout for linear regression. We prove that ablated data augmentation is equivalent to optimizing the ordinary least squares objective along with a penalty that we call the Contribution Covariance Penalty and inverted dropout, a more common implementation than dropout in popular frameworks, is equivalent to optimizing the ordinary least squares objective along with Modified L2. For deep networks, we demonstrate an empirical version of the result if we replace contributions with attributions and coefficients with average gradients, i.e., the Contribution Covariance Penalty and Modified L2 Penalty drop with the increase of the corresponding ablated data augmentation across a variety of networks.

The many Shapley values for model explanation

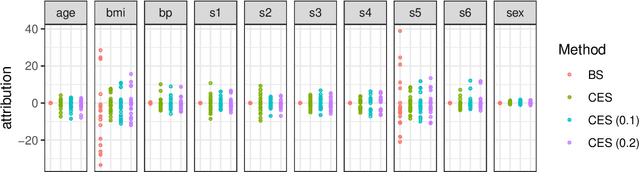
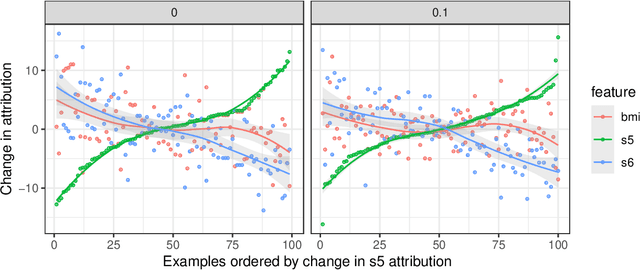
The Shapley value has become a popular method to attribute the prediction of a machine-learning model on an input to its base features. The Shapley value [1] is known to be the unique method that satisfies certain desirable properties, and this motivates its use. Unfortunately, despite this uniqueness result, there are a multiplicity of Shapley values used in explaining a model's prediction. This is because there are many ways to apply the Shapley value that differ in how they reference the model, the training data, and the explanation context. In this paper, we study an approach that applies the Shapley value to conditional expectations (CES) of sets of features (cf. [2]) that subsumes several prior approaches within a common framework. We provide the first algorithm for the general version of CES. We show that CES can result in counterintuitive attributions in theory and in practice (we study a diabetes prediction task); for instance, CES can assign non-zero attributions to features that are not referenced by the model. In contrast, we show that an approach called the Baseline Shapley (BS) does not exhibit counterintuitive attributions; we support this claim with a uniqueness (axiomatic) result. We show that BS is a special case of CES, and CES with an independent feature distribution coincides with a randomized version of BS. Thus, BS fits into the CES framework, but does not suffer from many of CES's deficiencies.

Feedback Detection for Live Predictors

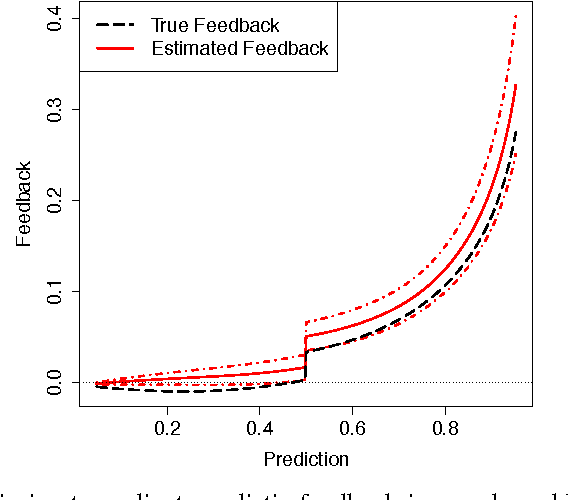
A predictor that is deployed in a live production system may perturb the features it uses to make predictions. Such a feedback loop can occur, for example, when a model that predicts a certain type of behavior ends up causing the behavior it predicts, thus creating a self-fulfilling prophecy. In this paper we analyze predictor feedback detection as a causal inference problem, and introduce a local randomization scheme that can be used to detect non-linear feedback in real-world problems. We conduct a pilot study for our proposed methodology using a predictive system currently deployed as a part of a search engine.