The many Shapley values for model explanation
Paper and Code
Aug 22, 2019
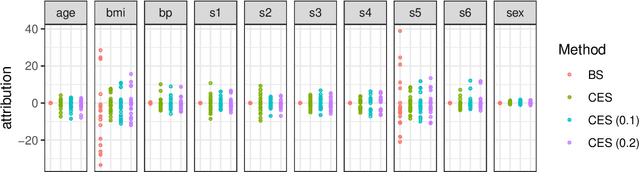

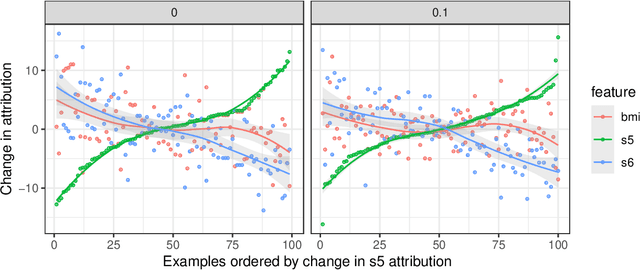
The Shapley value has become a popular method to attribute the prediction of a machine-learning model on an input to its base features. The Shapley value [1] is known to be the unique method that satisfies certain desirable properties, and this motivates its use. Unfortunately, despite this uniqueness result, there are a multiplicity of Shapley values used in explaining a model's prediction. This is because there are many ways to apply the Shapley value that differ in how they reference the model, the training data, and the explanation context. In this paper, we study an approach that applies the Shapley value to conditional expectations (CES) of sets of features (cf. [2]) that subsumes several prior approaches within a common framework. We provide the first algorithm for the general version of CES. We show that CES can result in counterintuitive attributions in theory and in practice (we study a diabetes prediction task); for instance, CES can assign non-zero attributions to features that are not referenced by the model. In contrast, we show that an approach called the Baseline Shapley (BS) does not exhibit counterintuitive attributions; we support this claim with a uniqueness (axiomatic) result. We show that BS is a special case of CES, and CES with an independent feature distribution coincides with a randomized version of BS. Thus, BS fits into the CES framework, but does not suffer from many of CES's deficiencies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge