Alyssa Pierson
Multi-robot Task Assignment for Aerial Tracking with Viewpoint Constraints
May 31, 2022
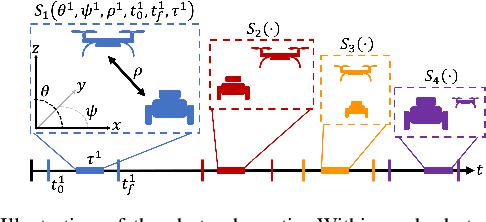
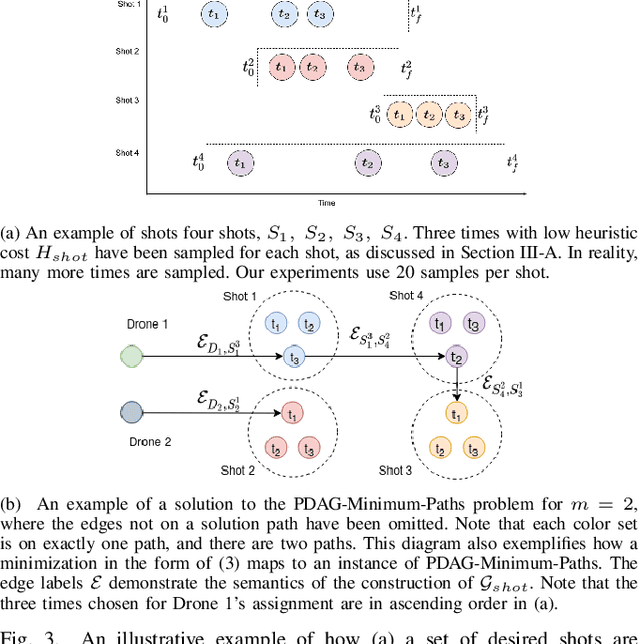
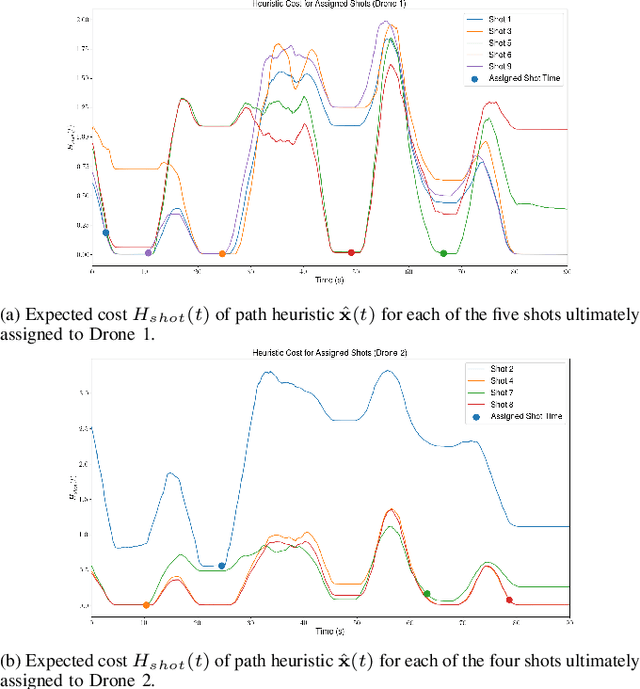
Abstract:We address the problem of assigning a team of drones to autonomously capture a set desired shots of a dynamic target in the presence of obstacles. We present a two-stage planning pipeline that generates offline an assignment of drone to shots and locally optimizes online the viewpoint. Given desired shot parameters, the high-level planner uses a visibility heuristic to predict good times for capturing each shot and uses an Integer Linear Program to compute drone assignments. An online Model Predictive Control algorithm uses the assignments as reference to capture the shots. The algorithm is validated in hardware with a pair of drones and a remote controlled car.
Free-Space Ellipsoid Graphs for Multi-Agent Target Monitoring
May 31, 2022

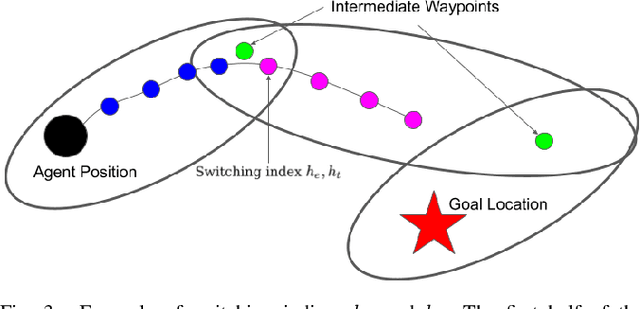
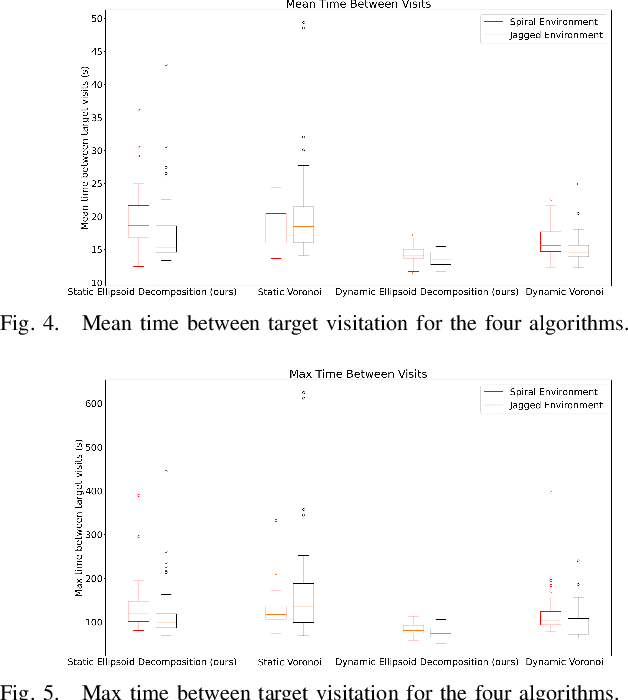
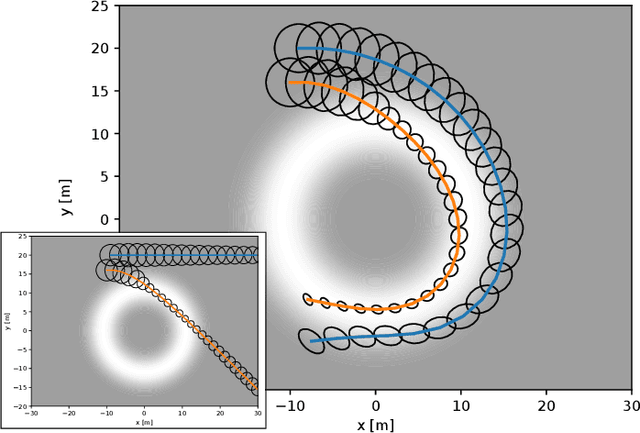
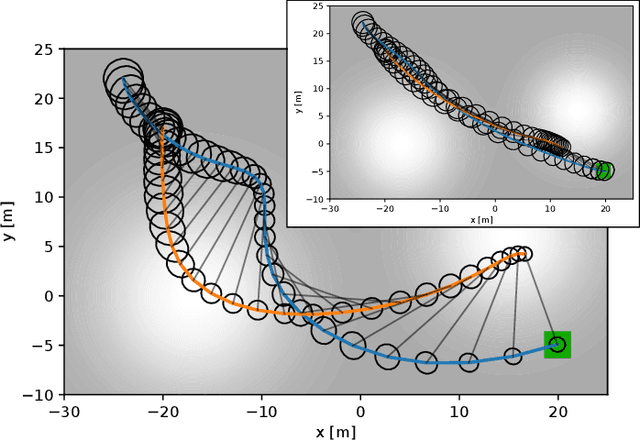
Abstract:We apply a novel framework for decomposing and reasoning about free space in an environment to a multi-agent persistent monitoring problem. Our decomposition method represents free space as a collection of ellipsoids associated with a weighted connectivity graph. The same ellipsoids used for reasoning about connectivity and distance during high level planning can be used as state constraints in a Model Predictive Control algorithm to enforce collision-free motion. This structure allows for streamlined implementation in distributed multi-agent tasks in 2D and 3D environments. We illustrate its effectiveness for a team of tracking agents tasked with monitoring a group of target agents. Our algorithm uses the ellipsoid decomposition as a primitive for the coordination, path planning, and control of the tracking agents. Simulations with four tracking agents monitoring fifteen dynamic targets in obstacle-rich environments demonstrate the performance of our algorithm.
Stochastic Dynamic Games in Belief Space
Sep 16, 2019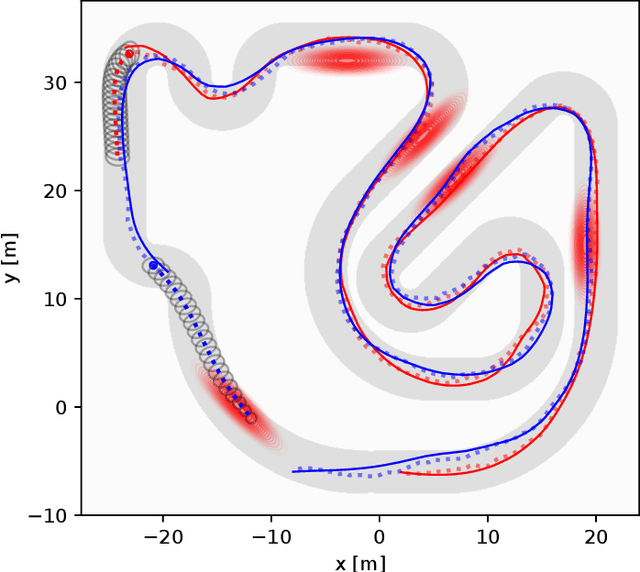

Abstract:Information gathering while interacting with other agents is critical in many emerging domains, such as self-driving cars, service robots, drone racing, and active surveillance. In these interactions, the interests of agents may be at odds with others, resulting in a non-cooperative dynamic game. Since unveiling one's own strategy to adversaries is undesirable, each agent must independently predict the other agents' future actions without communication. In the face of uncertainty from sensor and actuator noise, agents have to gain information over their own state, the states of others, and the environment. They must also consider how their own actions reveal information to others. We formulate this non-cooperative multi-agent planning problem as a stochastic dynamic game. Our solution uses local iterative dynamic programming in the belief space to find a Nash equilibrium of the game. We present three applications: active surveillance, guiding eyes for a blind agent, and autonomous racing. Agents with game-theoretic belief space planning win 44% more races compared to a baseline without game theory and 34% more than without belief space planning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge