The Monte Carlo Transformer: a stochastic self-attention model for sequence prediction

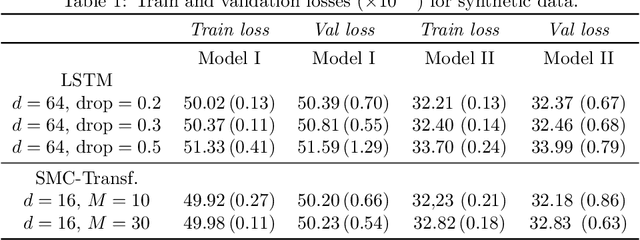
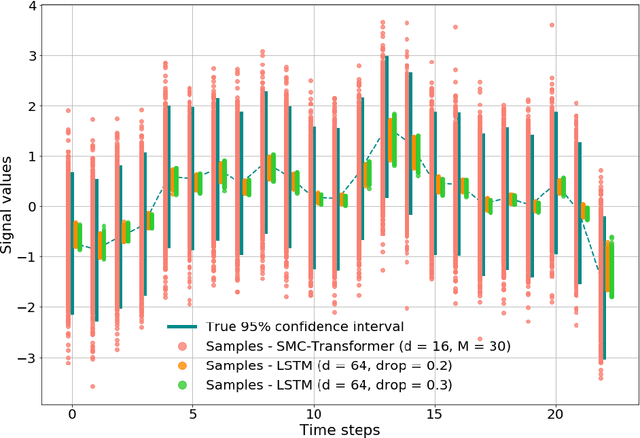
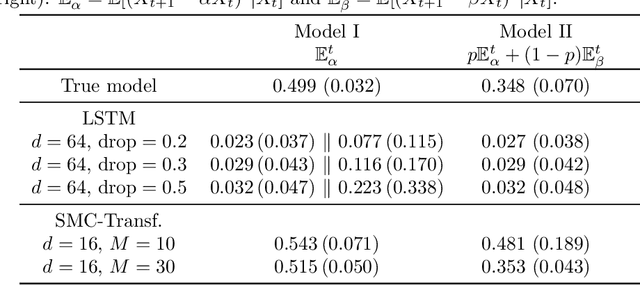
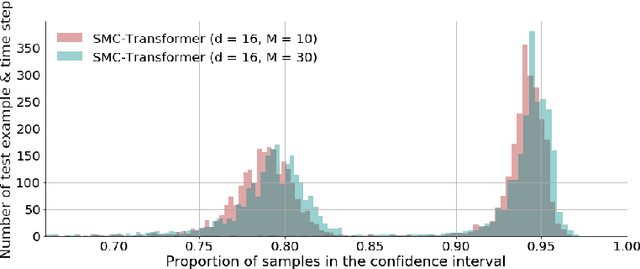
This paper introduces the Sequential Monte Carlo Transformer, an original approach that naturally captures the observations distribution in a recurrent architecture. The keys, queries, values and attention vectors of the network are considered as the unobserved stochastic states of its hidden structure. This generative model is such that at each time step the received observation is a random function of these past states in a given attention window. In this general state-space setting, we use Sequential Monte Carlo methods to approximate the posterior distributions of the states given the observations, and then to estimate the gradient of the log-likelihood. We thus propose a generative model providing a predictive distribution, instead of a single-point estimate.

On Last-Layer Algorithms for Classification: Decoupling Representation from Uncertainty Estimation

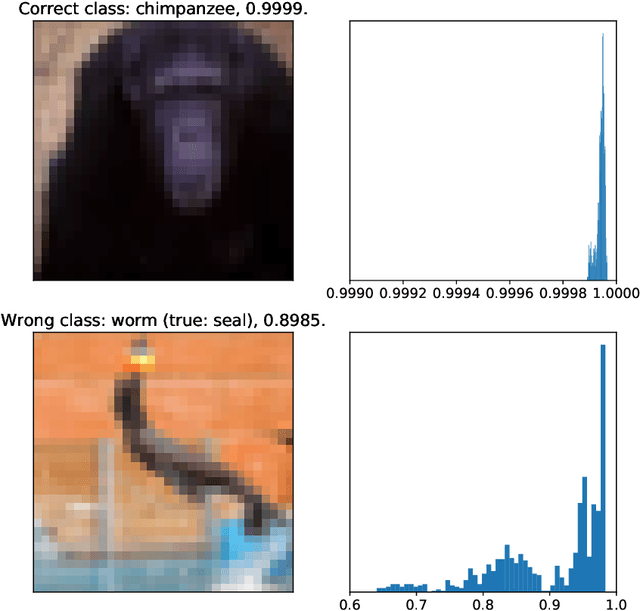
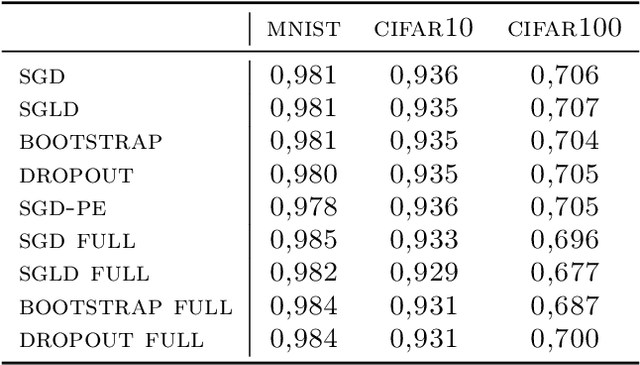
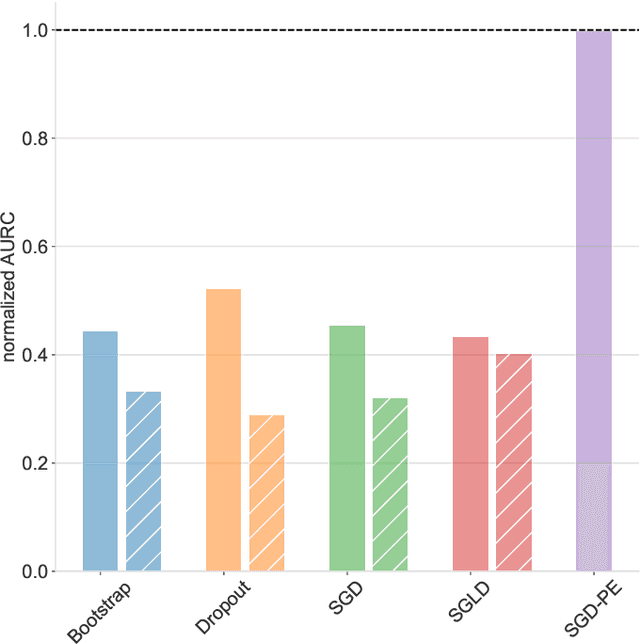
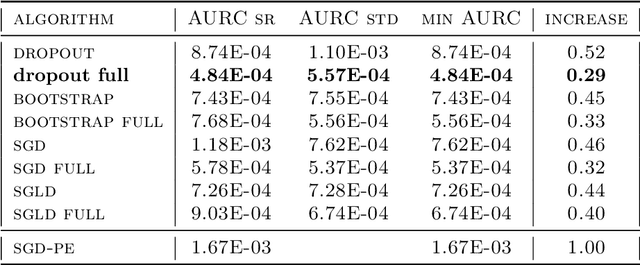
Uncertainty quantification for deep learning is a challenging open problem. Bayesian statistics offer a mathematically grounded framework to reason about uncertainties; however, approximate posteriors for modern neural networks still require prohibitive computational costs. We propose a family of algorithms which split the classification task into two stages: representation learning and uncertainty estimation. We compare four specific instances, where uncertainty estimation is performed via either an ensemble of Stochastic Gradient Descent or Stochastic Gradient Langevin Dynamics snapshots, an ensemble of bootstrapped logistic regressions, or via a number of Monte Carlo Dropout passes. We evaluate their performance in terms of \emph{selective} classification (risk-coverage), and their ability to detect out-of-distribution samples. Our experiments suggest there is limited value in adding multiple uncertainty layers to deep classifiers, and we observe that these simple methods strongly outperform a vanilla point-estimate SGD in some complex benchmarks like ImageNet.