Latent Factor Analysis of Gaussian Distributions under Graphical Constraints

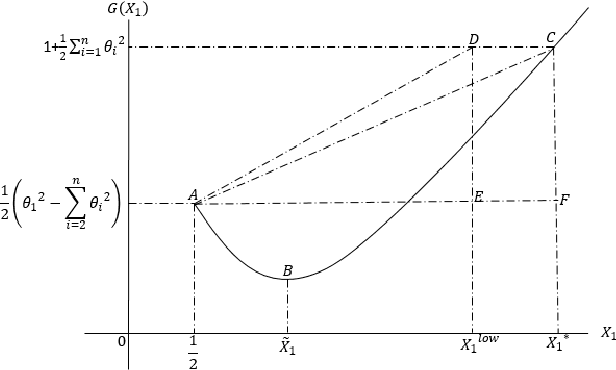
We explore the algebraic structure of the solution space of convex optimization problem Constrained Minimum Trace Factor Analysis (CMTFA), when the population covariance matrix $\Sigma_x$ has an additional latent graphical constraint, namely, a latent star topology. In particular, we have shown that CMTFA can have either a rank $ 1 $ or a rank $ n-1 $ solution and nothing in between. The special case of a rank $ 1 $ solution, corresponds to the case where just one latent variable captures all the dependencies among the observables, giving rise to a star topology. We found explicit conditions for both rank $ 1 $ and rank $n- 1$ solutions for CMTFA solution of $\Sigma_x$. As a basic attempt towards building a more general Gaussian tree, we have found a necessary and a sufficient condition for multiple clusters, each having rank $ 1 $ CMTFA solution, to satisfy a minimum probability to combine together to build a Gaussian tree. To support our analytical findings we have presented some numerical demonstrating the usefulness of the contributions of our work.

Synthesis of Gaussian Trees with Correlation Sign Ambiguity: An Information Theoretic Approach

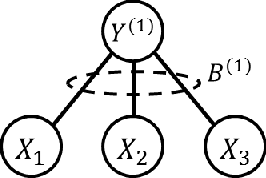
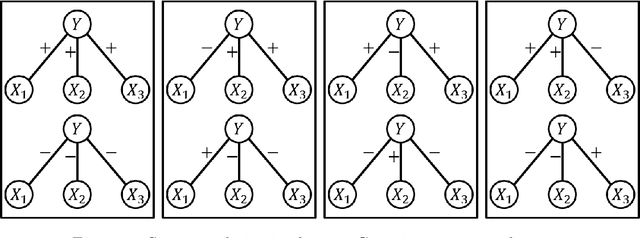
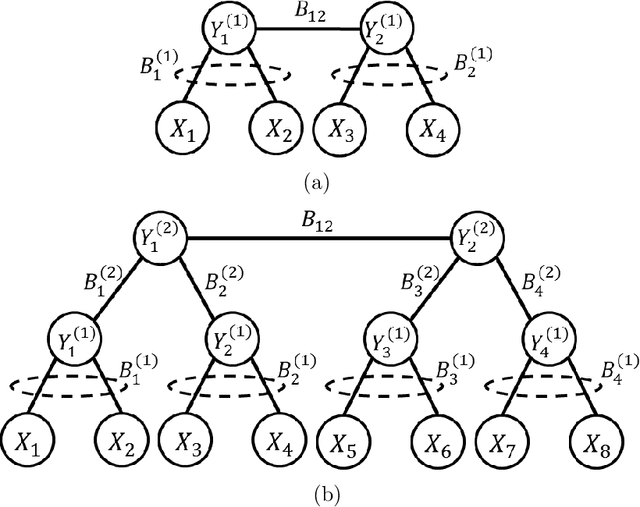
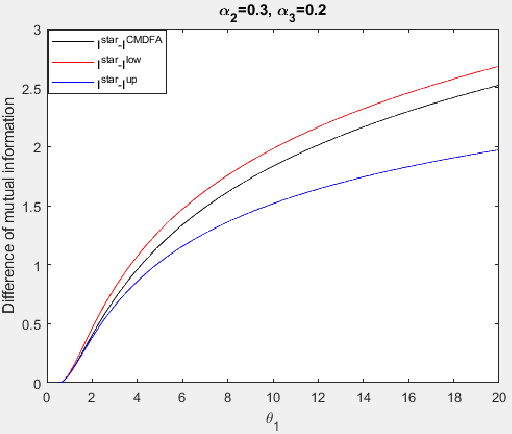
In latent Gaussian trees the pairwise correlation signs between the variables are intrinsically unrecoverable. Such information is vital since it completely determines the direction in which two variables are associated. In this work, we resort to information theoretical approaches to achieve two fundamental goals: First, we quantify the amount of information loss due to unrecoverable sign information. Second, we show the importance of such information in determining the maximum achievable rate region, in which the observed output vector can be synthesized, given its probability density function. In particular, we model the graphical model as a communication channel and propose a new layered encoding framework to synthesize observed data using upper layer Gaussian inputs and independent Bernoulli correlation sign inputs from each layer. We find the achievable rate region for the rate tuples of multi-layer latent Gaussian messages to synthesize the desired observables.