Synthesis of Gaussian Trees with Correlation Sign Ambiguity: An Information Theoretic Approach

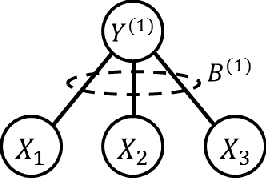
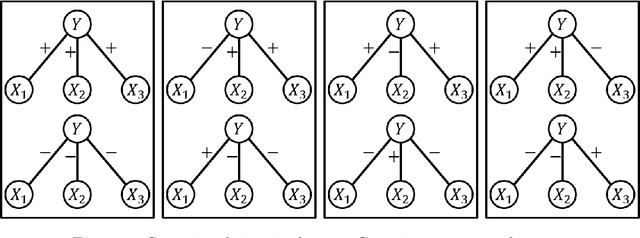
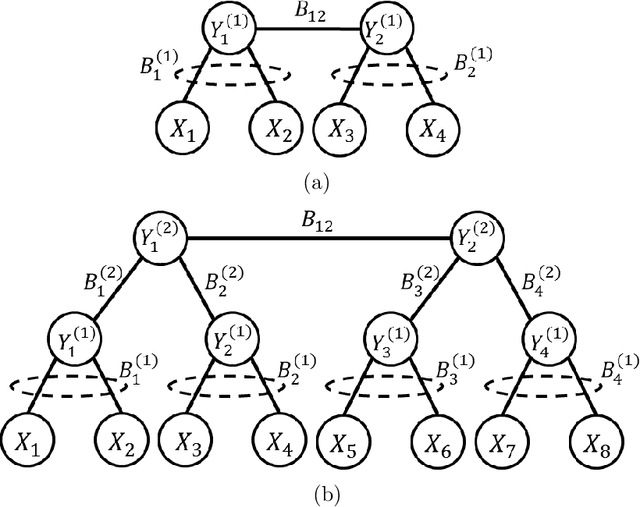
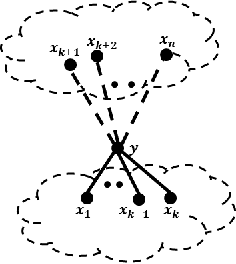
In latent Gaussian trees the pairwise correlation signs between the variables are intrinsically unrecoverable. Such information is vital since it completely determines the direction in which two variables are associated. In this work, we resort to information theoretical approaches to achieve two fundamental goals: First, we quantify the amount of information loss due to unrecoverable sign information. Second, we show the importance of such information in determining the maximum achievable rate region, in which the observed output vector can be synthesized, given its probability density function. In particular, we model the graphical model as a communication channel and propose a new layered encoding framework to synthesize observed data using upper layer Gaussian inputs and independent Bernoulli correlation sign inputs from each layer. We find the achievable rate region for the rate tuples of multi-layer latent Gaussian messages to synthesize the desired observables.