Latent Factor Analysis of Gaussian Distributions under Graphical Constraints
Paper and Code
Jan 11, 2020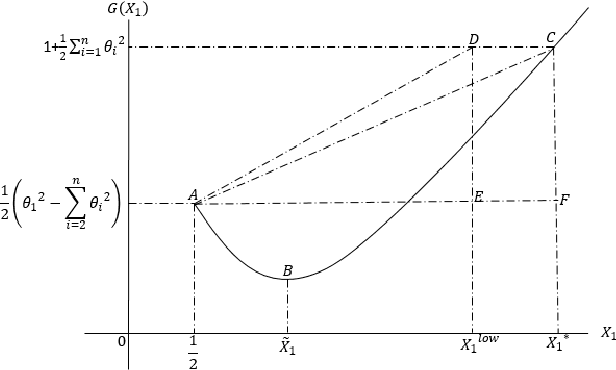
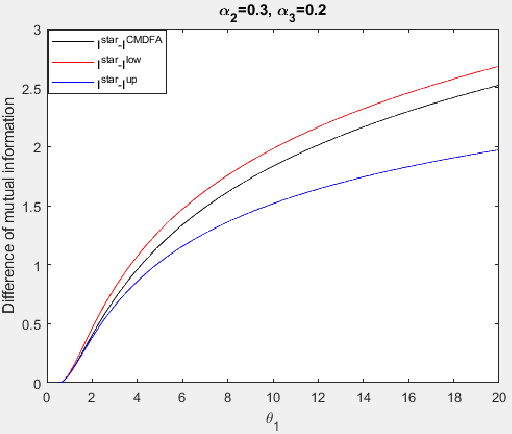
We explore the algebraic structure of the solution space of convex optimization problem Constrained Minimum Trace Factor Analysis (CMTFA), when the population covariance matrix $\Sigma_x$ has an additional latent graphical constraint, namely, a latent star topology. In particular, we have shown that CMTFA can have either a rank $ 1 $ or a rank $ n-1 $ solution and nothing in between. The special case of a rank $ 1 $ solution, corresponds to the case where just one latent variable captures all the dependencies among the observables, giving rise to a star topology. We found explicit conditions for both rank $ 1 $ and rank $n- 1$ solutions for CMTFA solution of $\Sigma_x$. As a basic attempt towards building a more general Gaussian tree, we have found a necessary and a sufficient condition for multiple clusters, each having rank $ 1 $ CMTFA solution, to satisfy a minimum probability to combine together to build a Gaussian tree. To support our analytical findings we have presented some numerical demonstrating the usefulness of the contributions of our work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge