Ali Hossein Gharari Foomani
MENSA: A Multi-Event Network for Survival Analysis under Informative Censoring
Sep 10, 2024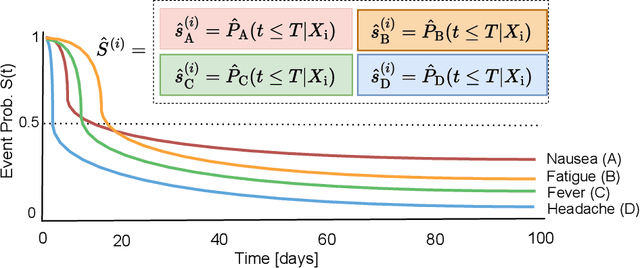

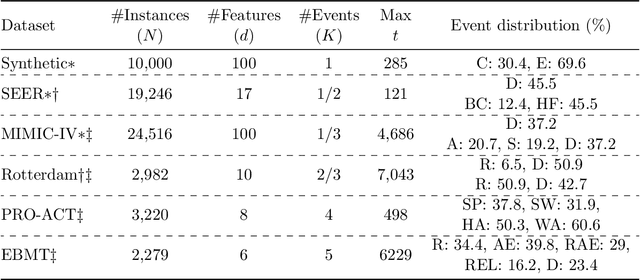
Abstract:Given an instance, a multi-event survival model predicts the time until that instance experiences each of several different events. These events are not mutually exclusive and there are often statistical dependencies between them. There are relatively few multi-event survival results, most focusing on producing a simple risk score, rather than the time-to-event itself. To overcome these issues, we introduce MENSA, a novel, deep learning approach for multi-event survival analysis that can jointly learn representations of the input covariates and the dependence structure between events. As a practical motivation for multi-event survival analysis, we consider the problem of predicting the time until a patient with amyotrophic lateral sclerosis (ALS) loses various physical functions, i.e., the ability to speak, swallow, write, or walk. When estimating when a patient is no longer able to swallow, our approach achieves an L1-Margin loss of 278.8 days, compared to 355.2 days when modeling each event separately. In addition, we also evaluate our approach in single-event and competing risk scenarios by modeling the censoring and event distributions as equal contributing factors in the optimization process, and show that our approach performs well across multiple benchmark datasets. The source code is available at: https://github.com/thecml/mensa
Copula-Based Deep Survival Models for Dependent Censoring
Jun 20, 2023
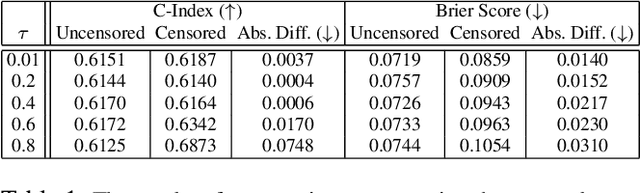
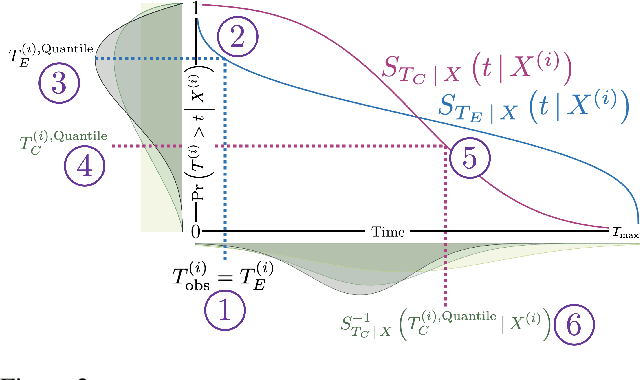
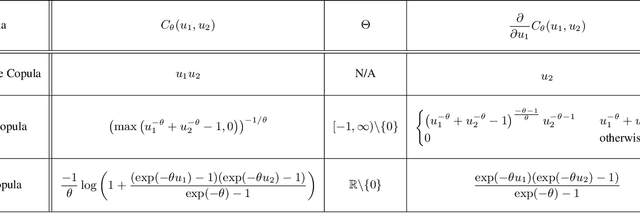
Abstract:A survival dataset describes a set of instances (e.g. patients) and provides, for each, either the time until an event (e.g. death), or the censoring time (e.g. when lost to follow-up - which is a lower bound on the time until the event). We consider the challenge of survival prediction: learning, from such data, a predictive model that can produce an individual survival distribution for a novel instance. Many contemporary methods of survival prediction implicitly assume that the event and censoring distributions are independent conditional on the instance's covariates - a strong assumption that is difficult to verify (as we observe only one outcome for each instance) and which can induce significant bias when it does not hold. This paper presents a parametric model of survival that extends modern non-linear survival analysis by relaxing the assumption of conditional independence. On synthetic and semi-synthetic data, our approach significantly improves estimates of survival distributions compared to the standard that assumes conditional independence in the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge