Copula-Based Deep Survival Models for Dependent Censoring
Paper and Code
Jun 20, 2023
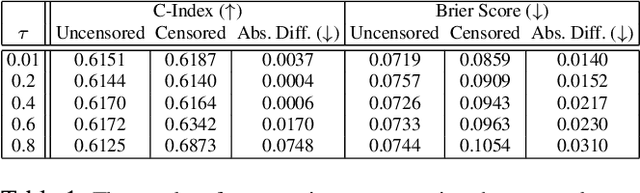
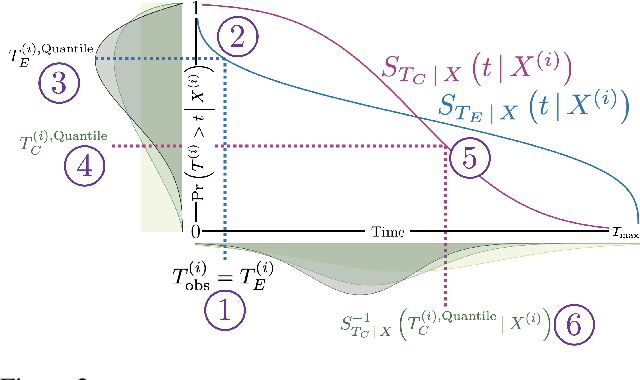
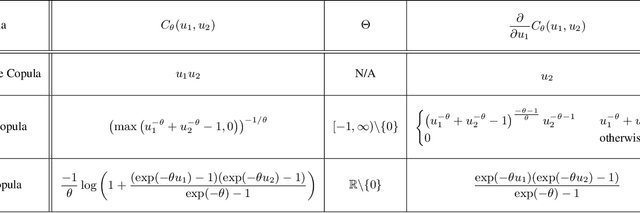
A survival dataset describes a set of instances (e.g. patients) and provides, for each, either the time until an event (e.g. death), or the censoring time (e.g. when lost to follow-up - which is a lower bound on the time until the event). We consider the challenge of survival prediction: learning, from such data, a predictive model that can produce an individual survival distribution for a novel instance. Many contemporary methods of survival prediction implicitly assume that the event and censoring distributions are independent conditional on the instance's covariates - a strong assumption that is difficult to verify (as we observe only one outcome for each instance) and which can induce significant bias when it does not hold. This paper presents a parametric model of survival that extends modern non-linear survival analysis by relaxing the assumption of conditional independence. On synthetic and semi-synthetic data, our approach significantly improves estimates of survival distributions compared to the standard that assumes conditional independence in the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge