The Effect of Haptic Guidance during Robotic-assisted Motor Training is Modulated by Personality Traits

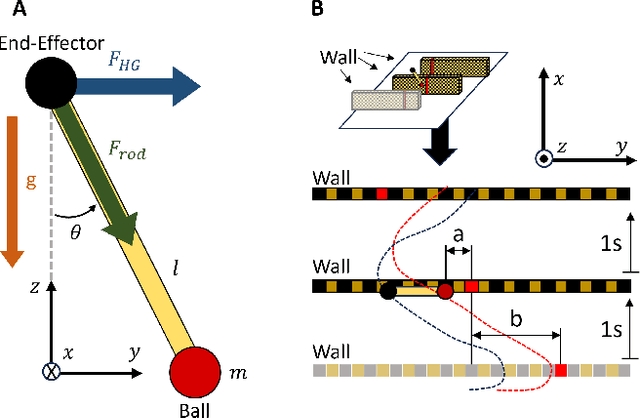
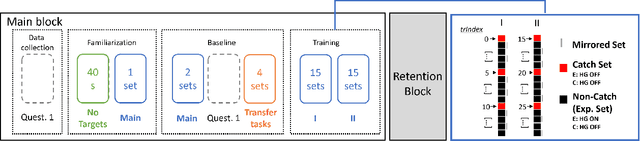
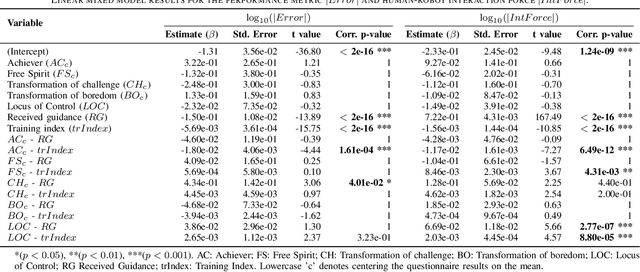
The provision of robotic assistance during motor training has proven to be effective in enhancing motor learning in some healthy trainee groups as well as patients. Personalizing such robotic assistance can help further improve motor (re)learning outcomes and cater better to the trainee's needs and desires. However, the development of personalized haptic assistance is hindered by the lack of understanding of the link between the trainee's personality and the effects of haptic guidance during human-robot interaction. To address this gap, we ran an experiment with 42 healthy participants who trained with a robotic device to control a virtual pendulum to hit incoming targets either with or without haptic guidance. We found that certain personal traits affected how users adapt and interact with the guidance during training. In particular, those participants with an 'Achiever gaming style' performed better and applied lower interaction forces to the robotic device than the average participant as the training progressed. Conversely, participants with the 'Free spirit game style' increased the interaction force in the course of training. We also found an interaction between some personal characteristics and haptic guidance. Specifically, participants with a higher 'Transformation of challenge' trait exhibited poorer performance during training while receiving haptic guidance compared to an average participant receiving haptic guidance. Furthermore, individuals with an external Locus of Control tended to increase their interaction force with the device, deviating from the pattern observed in an average participant under the same guidance. These findings suggest that individual characteristics may play a crucial role in the effectiveness of haptic guidance training strategies.

Testing for equality between conditional copulas given discretized conditioning events

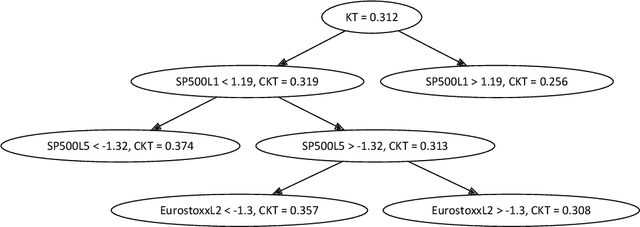
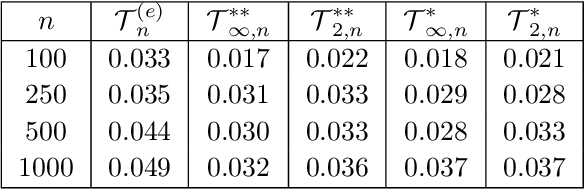
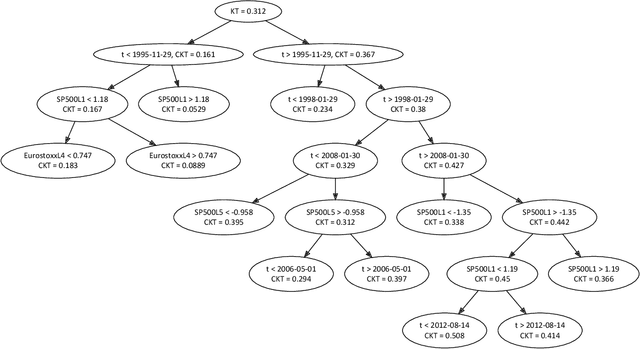
Several procedures have been recently proposed to test the simplifying assumption for conditional copulas. Instead of considering pointwise conditioning events, we study the constancy of the conditional dependence structure when some covariates belong to general borelian conditioning subsets. Several test statistics based on the equality of conditional Kendall's tau are introduced, and we derive their asymptotic distributions under the null. When such conditioning events are not fixed ex ante, we propose a data-driven procedure to recursively build such relevant subsets. It is based on decision trees that maximize the differences between the conditional Kendall's taus corresponding to the leaves of the trees. The performances of such tests are illustrated in a simulation experiment. Moreover, a study of the conditional dependence between financial stock returns is managed, given some clustering of their past values. The last application deals with the conditional dependence between coverage amounts in an insurance dataset.

On lower bounds for the bias-variance trade-off

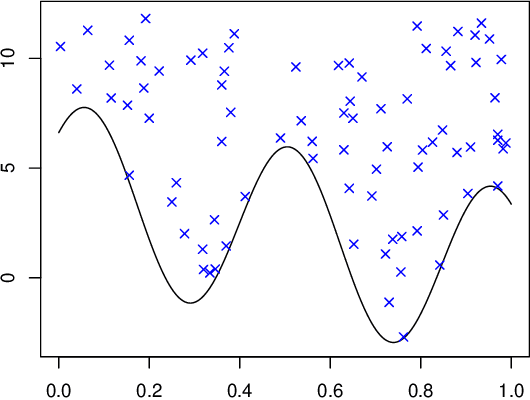
It is a common phenomenon that for high-dimensional and nonparametric statistical models, rate-optimal estimators balance squared bias and variance. Although this balancing is widely observed, little is known whether methods exist that could avoid the trade-off between bias and variance. We propose a general strategy to obtain lower bounds on the variance of any estimator with bias smaller than a prespecified bound. This shows to which extent the bias-variance trade-off is unavoidable and allows to quantify the loss of performance for methods that do not obey it. The approach is based on a number of abstract lower bounds for the variance involving the change of expectation with respect to different probability measures as well as information measures such as the Kullback-Leibler or chi-square divergence. Some of these inequalities rely on a new concept of information matrices. In a second part of the article, the abstract lower bounds are applied to several statistical models including the Gaussian white noise model, a boundary estimation problem, the Gaussian sequence model and the high-dimensional linear regression model. For these specific statistical applications, different types of bias-variance trade-offs occur that vary considerably in their strength. For the trade-off between integrated squared bias and integrated variance in the Gaussian white noise model, we propose to combine the general strategy for lower bounds with a reduction technique. This allows us to reduce the original problem to a lower bound on the bias-variance trade-off for estimators with additional symmetry properties in a simpler statistical model. To highlight possible extensions of the proposed framework, we moreover briefly discuss the trade-off between bias and mean absolute deviation.

A classification point-of-view about conditional Kendall's tau

We show how the problem of estimating conditional Kendall's tau can be rewritten as a classification task. Conditional Kendall's tau is a conditional dependence parameter that is a characteristic of a given pair of random variables. The goal is to predict whether the pair is concordant (value of $1$) or discordant (value of $-1$) conditionally on some covariates. We prove the consistency and the asymptotic normality of a family of penalized approximate maximum likelihood estimators, including the equivalent of the logit and probit regressions in our framework. Then, we detail specific algorithms adapting usual machine learning techniques, including nearest neighbors, decision trees, random forests and neural networks, to the setting of the estimation of conditional Kendall's tau. A small simulation study compares their finite sample properties. Finally, we apply all these estimators to a dataset of European stock indices.