Testing for equality between conditional copulas given discretized conditioning events

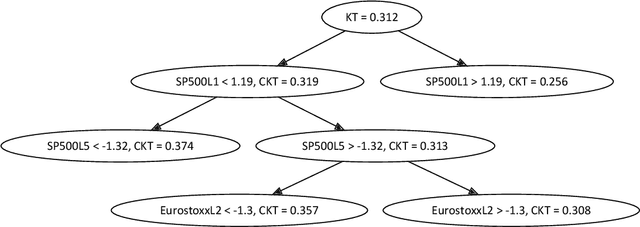
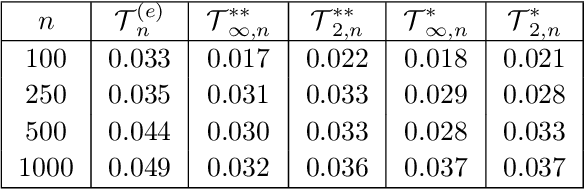
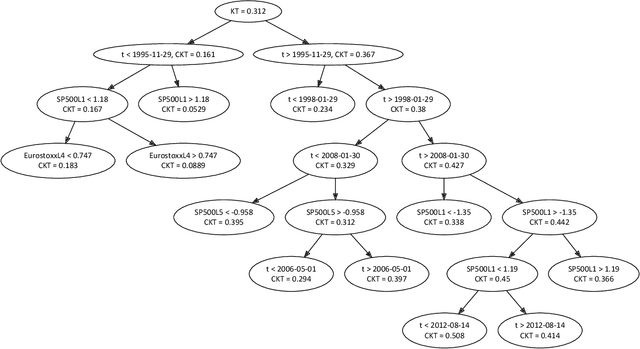
Several procedures have been recently proposed to test the simplifying assumption for conditional copulas. Instead of considering pointwise conditioning events, we study the constancy of the conditional dependence structure when some covariates belong to general borelian conditioning subsets. Several test statistics based on the equality of conditional Kendall's tau are introduced, and we derive their asymptotic distributions under the null. When such conditioning events are not fixed ex ante, we propose a data-driven procedure to recursively build such relevant subsets. It is based on decision trees that maximize the differences between the conditional Kendall's taus corresponding to the leaves of the trees. The performances of such tests are illustrated in a simulation experiment. Moreover, a study of the conditional dependence between financial stock returns is managed, given some clustering of their past values. The last application deals with the conditional dependence between coverage amounts in an insurance dataset.

A classification point-of-view about conditional Kendall's tau

We show how the problem of estimating conditional Kendall's tau can be rewritten as a classification task. Conditional Kendall's tau is a conditional dependence parameter that is a characteristic of a given pair of random variables. The goal is to predict whether the pair is concordant (value of $1$) or discordant (value of $-1$) conditionally on some covariates. We prove the consistency and the asymptotic normality of a family of penalized approximate maximum likelihood estimators, including the equivalent of the logit and probit regressions in our framework. Then, we detail specific algorithms adapting usual machine learning techniques, including nearest neighbors, decision trees, random forests and neural networks, to the setting of the estimation of conditional Kendall's tau. A small simulation study compares their finite sample properties. Finally, we apply all these estimators to a dataset of European stock indices.