Contextual Stochastic Vehicle Routing with Time Windows

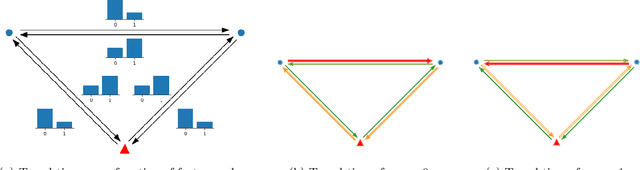
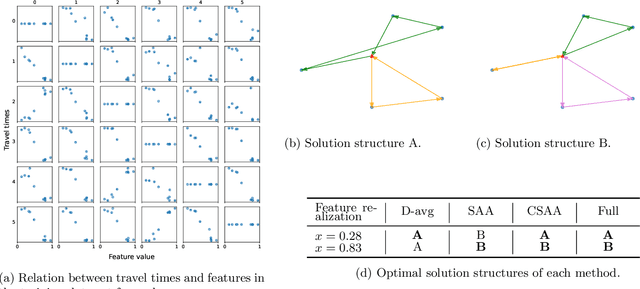
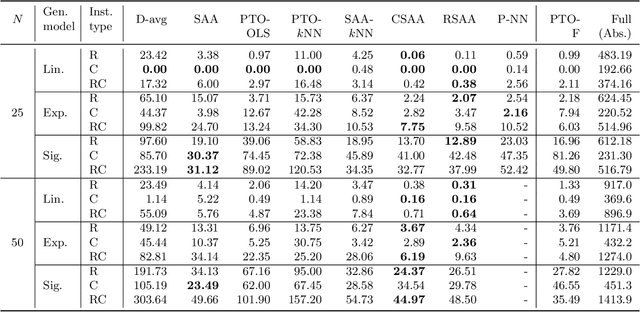
We study the vehicle routing problem with time windows (VRPTW) and stochastic travel times, in which the decision-maker observes related contextual information, represented as feature variables, before making routing decisions. Despite the extensive literature on stochastic VRPs, the integration of feature variables has received limited attention in this context. We introduce the contextual stochastic VRPTW, which minimizes the total transportation cost and expected late arrival penalties conditioned on the observed features. Since the joint distribution of travel times and features is unknown, we present novel data-driven prescriptive models that use historical data to provide an approximate solution to the problem. We distinguish the prescriptive models between point-based approximation, sample average approximation, and penalty-based approximation, each taking a different perspective on dealing with stochastic travel times and features. We develop specialized branch-price-and-cut algorithms to solve these data-driven prescriptive models. In our computational experiments, we compare the out-of-sample cost performance of different methods on instances with up to one hundred customers. Our results show that, surprisingly, a feature-dependent sample average approximation outperforms existing and novel methods in most settings.

Optimal Decision Diagrams for Classification

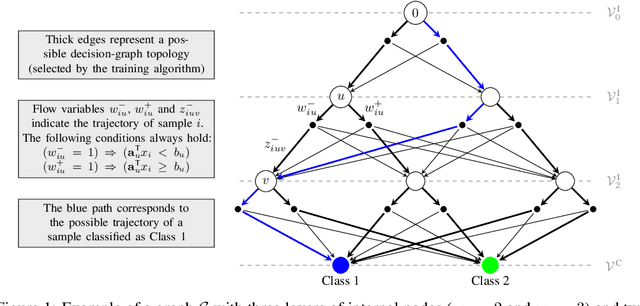
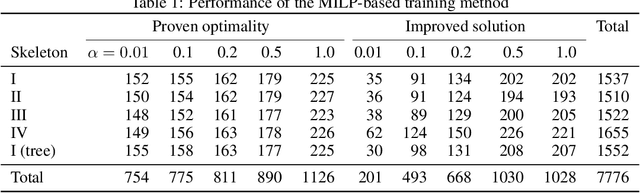
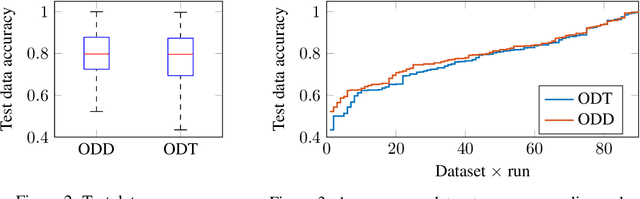
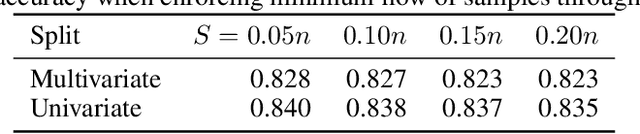
Decision diagrams for classification have some notable advantages over decision trees, as their internal connections can be determined at training time and their width is not bound to grow exponentially with their depth. Accordingly, decision diagrams are usually less prone to data fragmentation in internal nodes. However, the inherent complexity of training these classifiers acted as a long-standing barrier to their widespread adoption. In this context, we study the training of optimal decision diagrams (ODDs) from a mathematical programming perspective. We introduce a novel mixed-integer linear programming model for training and demonstrate its applicability for many datasets of practical importance. Further, we show how this model can be easily extended for fairness, parsimony, and stability notions. We present numerical analyses showing that our model allows training ODDs in short computational times, and that ODDs achieve better accuracy than optimal decision trees, while allowing for improved stability without significant accuracy losses.