Contextual Stochastic Vehicle Routing with Time Windows
Paper and Code
Feb 10, 2024
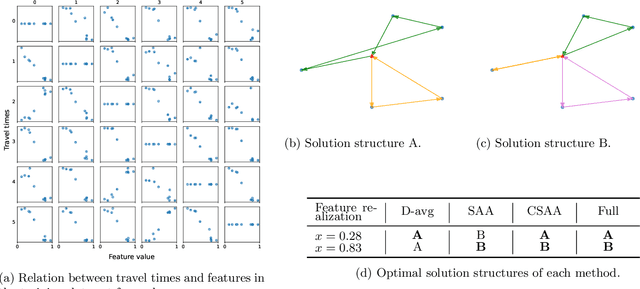
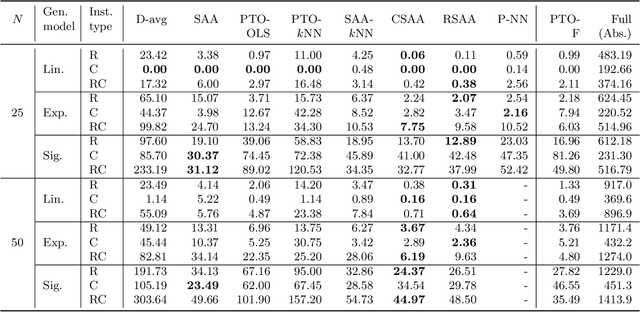
We study the vehicle routing problem with time windows (VRPTW) and stochastic travel times, in which the decision-maker observes related contextual information, represented as feature variables, before making routing decisions. Despite the extensive literature on stochastic VRPs, the integration of feature variables has received limited attention in this context. We introduce the contextual stochastic VRPTW, which minimizes the total transportation cost and expected late arrival penalties conditioned on the observed features. Since the joint distribution of travel times and features is unknown, we present novel data-driven prescriptive models that use historical data to provide an approximate solution to the problem. We distinguish the prescriptive models between point-based approximation, sample average approximation, and penalty-based approximation, each taking a different perspective on dealing with stochastic travel times and features. We develop specialized branch-price-and-cut algorithms to solve these data-driven prescriptive models. In our computational experiments, we compare the out-of-sample cost performance of different methods on instances with up to one hundred customers. Our results show that, surprisingly, a feature-dependent sample average approximation outperforms existing and novel methods in most settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge