On Approaches to Building Surrogate ODE Models for Diffusion Bridges

Diffusion and Schrödinger Bridge models have established state-of-the-art performance in generative modeling but are often hampered by significant computational costs and complex training procedures. While continuous-time bridges promise faster sampling, overparameterized neural networks describe their optimal dynamics, and the underlying stochastic differential equations can be difficult to integrate efficiently. This work introduces a novel paradigm that uses surrogate models to create simpler, faster, and more flexible approximations of these dynamics. We propose two specific algorithms: SINDy Flow Matching (SINDy-FM), which leverages sparse regression to identify interpretable, symbolic differential equations from data, and a Neural-ODE reformulation of the Schrödinger Bridge (DSBM-NeuralODE) for flexible continuous-time parameterization. Our experiments on Gaussian transport tasks and MNIST latent translation demonstrate that these surrogates achieve competitive performance while offering dramatic improvements in efficiency and interpretability. The symbolic SINDy-FM models, in particular, reduce parameter counts by several orders of magnitude and enable near-instantaneous inference, paving the way for a new class of tractable and high-performing bridge models for practical deployment.

Towards Universal Neural Operators through Multiphysics Pretraining

Although neural operators are widely used in data-driven physical simulations, their training remains computationally expensive. Recent advances address this issue via downstream learning, where a model pretrained on simpler problems is fine-tuned on more complex ones. In this research, we investigate transformer-based neural operators, which have previously been applied only to specific problems, in a more general transfer learning setting. We evaluate their performance across diverse PDE problems, including extrapolation to unseen parameters, incorporation of new variables, and transfer from multi-equation datasets. Our results demonstrate that advanced neural operator architectures can effectively transfer knowledge across PDE problems.

Knowledge-aware equation discovery with automated background knowledge extraction

In differential equation discovery algorithms, a priori expert knowledge is mainly used implicitly to constrain the form of the expected equation, making it impossible for the algorithm to truly discover equations. Instead, most differential equation discovery algorithms try to recover the coefficients for a known structure. In this paper, we describe an algorithm that allows the discovery of unknown equations using automatically or manually extracted background knowledge. Instead of imposing rigid constraints, we modify the structure space so that certain terms are likely to appear within the crossover and mutation operators. In this way, we mimic expertly chosen terms while preserving the possibility of obtaining any equation form. The paper shows that the extraction and use of knowledge allows it to outperform the SINDy algorithm in terms of search stability and robustness. Synthetic examples are given for Burgers, wave, and Korteweg--De Vries equations.

Towards stable real-world equation discovery with assessing differentiating quality influence

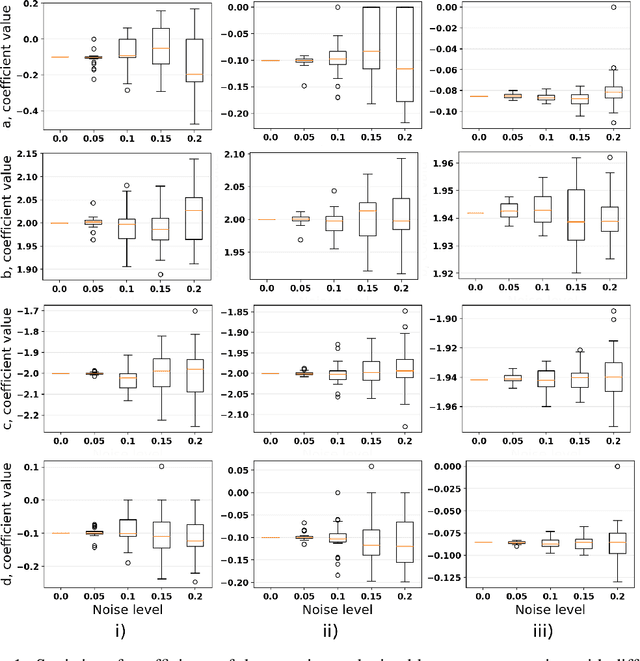
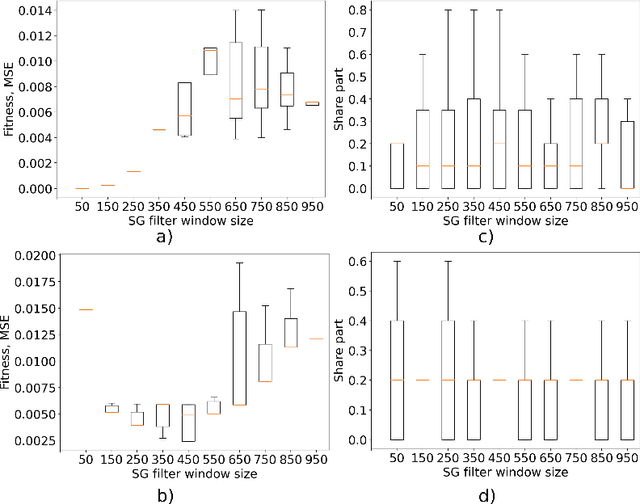
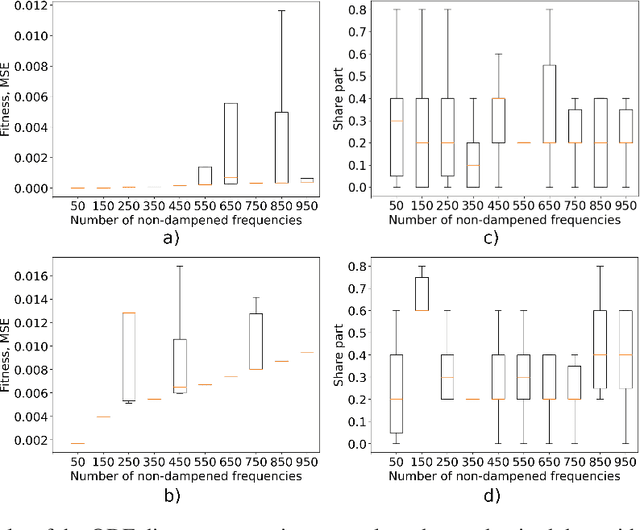
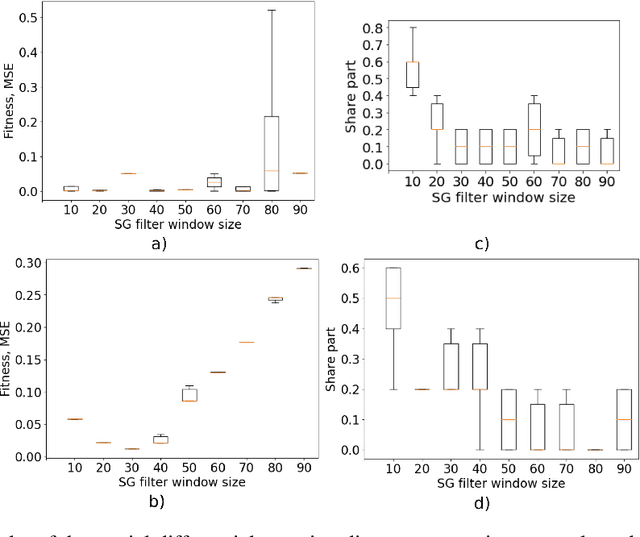
This paper explores the critical role of differentiation approaches for data-driven differential equation discovery. Accurate derivatives of the input data are essential for reliable algorithmic operation, particularly in real-world scenarios where measurement quality is inevitably compromised. We propose alternatives to the commonly used finite differences-based method, notorious for its instability in the presence of noise, which can exacerbate random errors in the data. Our analysis covers four distinct methods: Savitzky-Golay filtering, spectral differentiation, smoothing based on artificial neural networks, and the regularization of derivative variation. We evaluate these methods in terms of applicability to problems, similar to the real ones, and their ability to ensure the convergence of equation discovery algorithms, providing valuable insights for robust modeling of real-world processes.

Towards true discovery of the differential equations

Differential equation discovery, a machine learning subfield, is used to develop interpretable models, particularly in nature-related applications. By expertly incorporating the general parametric form of the equation of motion and appropriate differential terms, algorithms can autonomously uncover equations from data. This paper explores the prerequisites and tools for independent equation discovery without expert input, eliminating the need for equation form assumptions. We focus on addressing the challenge of assessing the adequacy of discovered equations when the correct equation is unknown, with the aim of providing insights for reliable equation discovery without prior knowledge of the equation form.

Directed differential equation discovery using modified mutation and cross-over operators

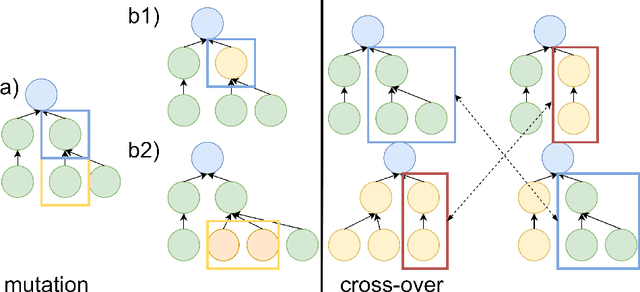
The discovery of equations with knowledge of the process origin is a tempting prospect. However, most equation discovery tools rely on gradient methods, which offer limited control over parameters. An alternative approach is the evolutionary equation discovery, which allows modification of almost every optimization stage. In this paper, we examine the modifications that can be introduced into the evolutionary operators of the equation discovery algorithm, taking inspiration from directed evolution techniques employed in fields such as chemistry and biology. The resulting approach, dubbed directed equation discovery, demonstrates a greater ability to converge towards accurate solutions than the conventional method. To support our findings, we present experiments based on Burgers', wave, and Korteweg--de Vries equations.

Comparison of Single- and Multi- Objective Optimization Quality for Evolutionary Equation Discovery

Evolutionary differential equation discovery proved to be a tool to obtain equations with less a priori assumptions than conventional approaches, such as sparse symbolic regression over the complete possible terms library. The equation discovery field contains two independent directions. The first one is purely mathematical and concerns differentiation, the object of optimization and its relation to the functional spaces and others. The second one is dedicated purely to the optimizational problem statement. Both topics are worth investigating to improve the algorithm's ability to handle experimental data a more artificial intelligence way, without significant pre-processing and a priori knowledge of their nature. In the paper, we consider the prevalence of either single-objective optimization, which considers only the discrepancy between selected terms in the equation, or multi-objective optimization, which additionally takes into account the complexity of the obtained equation. The proposed comparison approach is shown on classical model examples -- Burgers equation, wave equation, and Korteweg - de Vries equation.

On the balance between the training time and interpretability of neural ODE for time series modelling

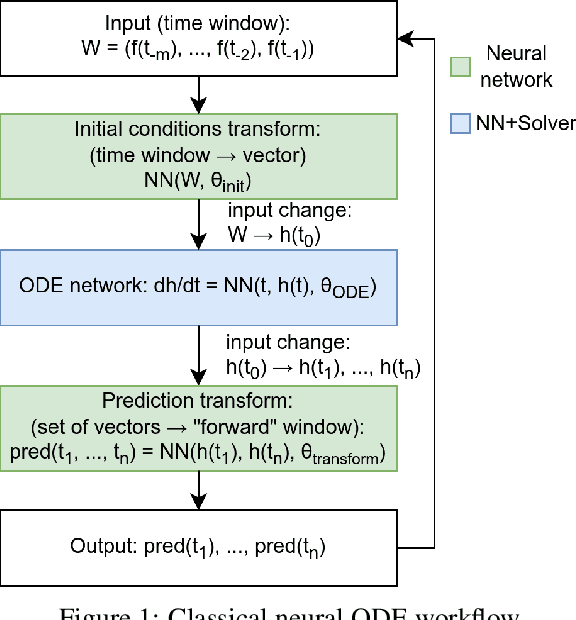
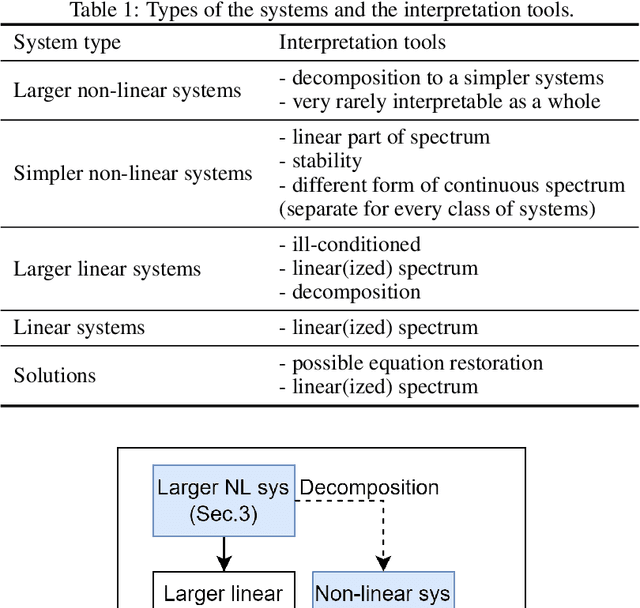
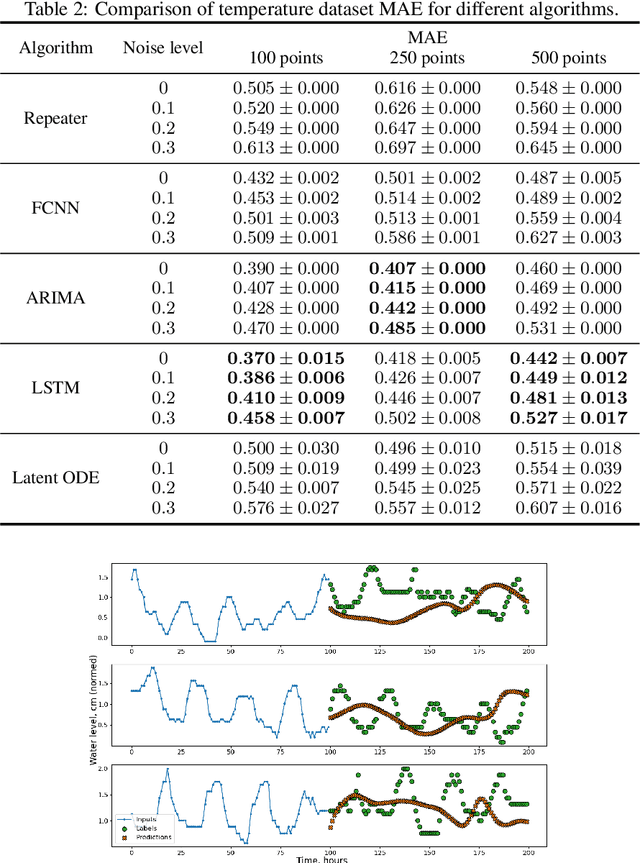
Most machine learning methods are used as a black box for modelling. We may try to extract some knowledge from physics-based training methods, such as neural ODE (ordinary differential equation). Neural ODE has advantages like a possibly higher class of represented functions, the extended interpretability compared to black-box machine learning models, ability to describe both trend and local behaviour. Such advantages are especially critical for time series with complicated trends. However, the known drawback is the high training time compared to the autoregressive models and long-short term memory (LSTM) networks widely used for data-driven time series modelling. Therefore, we should be able to balance interpretability and training time to apply neural ODE in practice. The paper shows that modern neural ODE cannot be reduced to simpler models for time-series modelling applications. The complexity of neural ODE is compared to or exceeds the conventional time-series modelling tools. The only interpretation that could be extracted is the eigenspace of the operator, which is an ill-posed problem for a large system. Spectra could be extracted using different classical analysis methods that do not have the drawback of extended time. Consequently, we reduce the neural ODE to a simpler linear form and propose a new view on time-series modelling using combined neural networks and an ODE system approach.

Automated differential equation solver based on the parametric approximation optimization

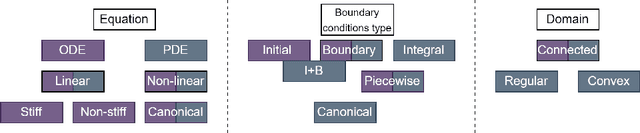
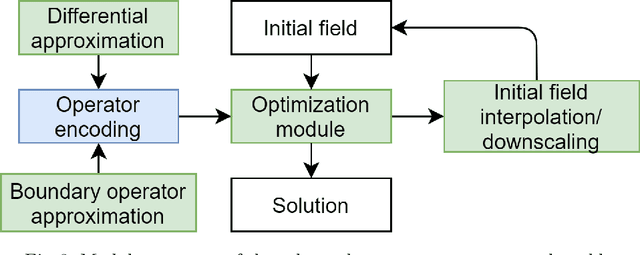
The numerical methods for differential equation solution allow obtaining a discrete field that converges towards the solution if the method is applied to the correct problem. Nevertheless, the numerical methods have the restricted class of the equations, on which the convergence with a given parameter set or range is proved. Only a few "cheap and dirty" numerical methods converge on a wide class of equations without parameter tuning with the lower approximation order price. The article presents a method that uses an optimization algorithm to obtain a solution using the parameterized approximation. The result may not be as precise as an expert one. However, it allows solving the wide class of equations in an automated manner without the algorithm's parameters change.

Model-agnostic multi-objective approach for the evolutionary discovery of mathematical models

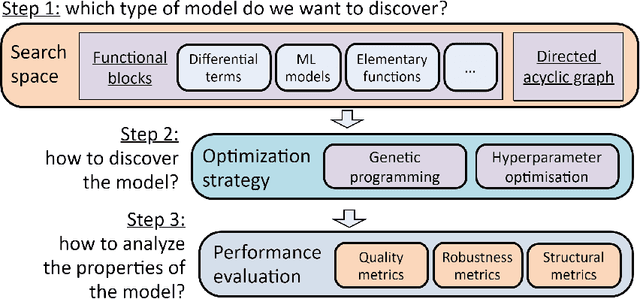
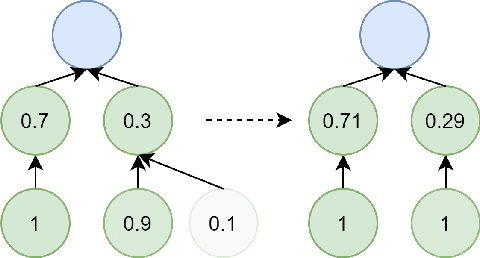
In modern data science, it is often not enough to obtain only a data-driven model with a good prediction quality. On the contrary, it is more interesting to understand the properties of the model, which parts could be replaced to obtain better results. Such questions are unified under machine learning interpretability questions, which could be considered one of the area's raising topics. In the paper, we use multi-objective evolutionary optimization for composite data-driven model learning to obtain the algorithm's desired properties. It means that whereas one of the apparent objectives is precision, the other could be chosen as the complexity of the model, robustness, and many others. The method application is shown on examples of multi-objective learning of composite models, differential equations, and closed-form algebraic expressions are unified and form approach for model-agnostic learning of the interpretable models.