Multi-objective discovery of PDE systems using evolutionary approach
Paper and Code
Mar 11, 2021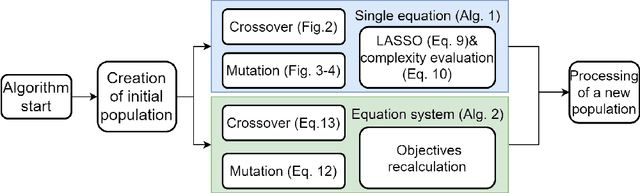
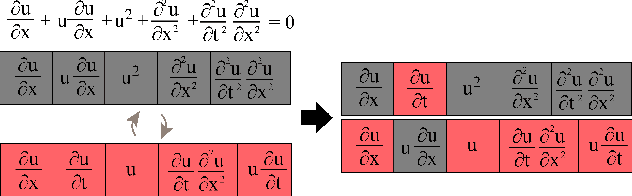
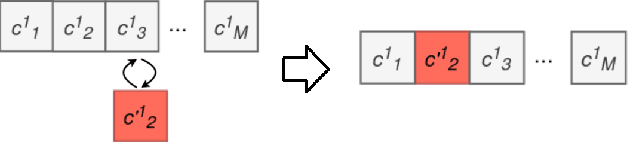

Usually, the systems of partial differential equations (PDEs) are discovered from observational data in the single vector equation form. However, this approach restricts the application to the real cases, where, for example, the form of the external forcing is of interest. In the paper, a multi-objective co-evolution algorithm is described. The single equations within the system and the system itself are evolved simultaneously to obtain the system. This approach allows discovering the systems with the form-independent equations. In contrast to the single vector equation, a component-wise system is more suitable for expert interpretation and, therefore, for applications. The example of the two-dimensional Navier-Stokes equation is considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge