Comparison of Single- and Multi- Objective Optimization Quality for Evolutionary Equation Discovery

Evolutionary differential equation discovery proved to be a tool to obtain equations with less a priori assumptions than conventional approaches, such as sparse symbolic regression over the complete possible terms library. The equation discovery field contains two independent directions. The first one is purely mathematical and concerns differentiation, the object of optimization and its relation to the functional spaces and others. The second one is dedicated purely to the optimizational problem statement. Both topics are worth investigating to improve the algorithm's ability to handle experimental data a more artificial intelligence way, without significant pre-processing and a priori knowledge of their nature. In the paper, we consider the prevalence of either single-objective optimization, which considers only the discrepancy between selected terms in the equation, or multi-objective optimization, which additionally takes into account the complexity of the obtained equation. The proposed comparison approach is shown on classical model examples -- Burgers equation, wave equation, and Korteweg - de Vries equation.

Model-agnostic multi-objective approach for the evolutionary discovery of mathematical models

In modern data science, it is often not enough to obtain only a data-driven model with a good prediction quality. On the contrary, it is more interesting to understand the properties of the model, which parts could be replaced to obtain better results. Such questions are unified under machine learning interpretability questions, which could be considered one of the area's raising topics. In the paper, we use multi-objective evolutionary optimization for composite data-driven model learning to obtain the algorithm's desired properties. It means that whereas one of the apparent objectives is precision, the other could be chosen as the complexity of the model, robustness, and many others. The method application is shown on examples of multi-objective learning of composite models, differential equations, and closed-form algebraic expressions are unified and form approach for model-agnostic learning of the interpretable models.

Multi-objective discovery of PDE systems using evolutionary approach

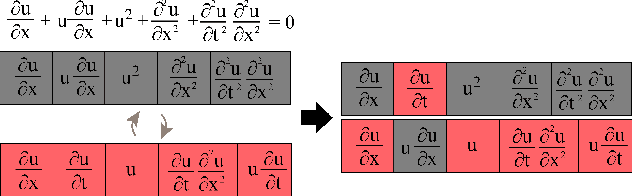
Usually, the systems of partial differential equations (PDEs) are discovered from observational data in the single vector equation form. However, this approach restricts the application to the real cases, where, for example, the form of the external forcing is of interest. In the paper, a multi-objective co-evolution algorithm is described. The single equations within the system and the system itself are evolved simultaneously to obtain the system. This approach allows discovering the systems with the form-independent equations. In contrast to the single vector equation, a component-wise system is more suitable for expert interpretation and, therefore, for applications. The example of the two-dimensional Navier-Stokes equation is considered.

The data-driven physical-based equations discovery using evolutionary approach

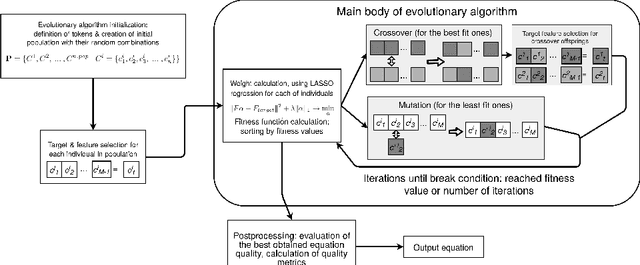
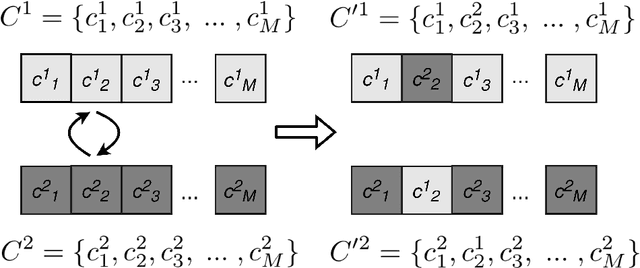
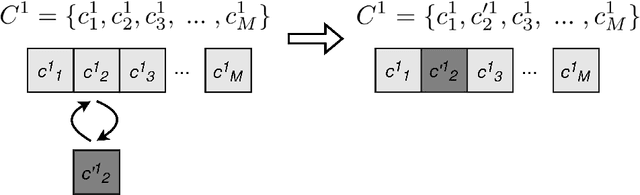
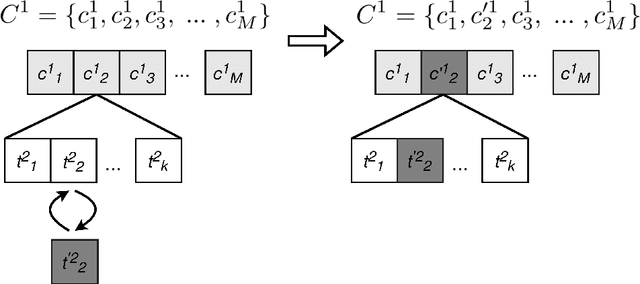
The modern machine learning methods allow one to obtain the data-driven models in various ways. However, the more complex the model is, the harder it is to interpret. In the paper, we describe the algorithm for the mathematical equations discovery from the given observations data. The algorithm combines genetic programming with the sparse regression. This algorithm allows obtaining different forms of the resulting models. As an example, it could be used for governing analytical equation discovery as well as for partial differential equations (PDE) discovery. The main idea is to collect a bag of the building blocks (it may be simple functions or their derivatives of arbitrary order) and consequently take them from the bag to create combinations, which will represent terms of the final equation. The selected terms pass to the evolutionary algorithm, which is used to evolve the selection. The evolutionary steps are combined with the sparse regression to pick only the significant terms. As a result, we obtain a short and interpretable expression that describes the physical process that lies beyond the data. In the paper, two examples of the algorithm application are described: the PDE discovery for the metocean processes and the function discovery for the acoustics.