Towards stable real-world equation discovery with assessing differentiating quality influence
Paper and Code
Nov 09, 2023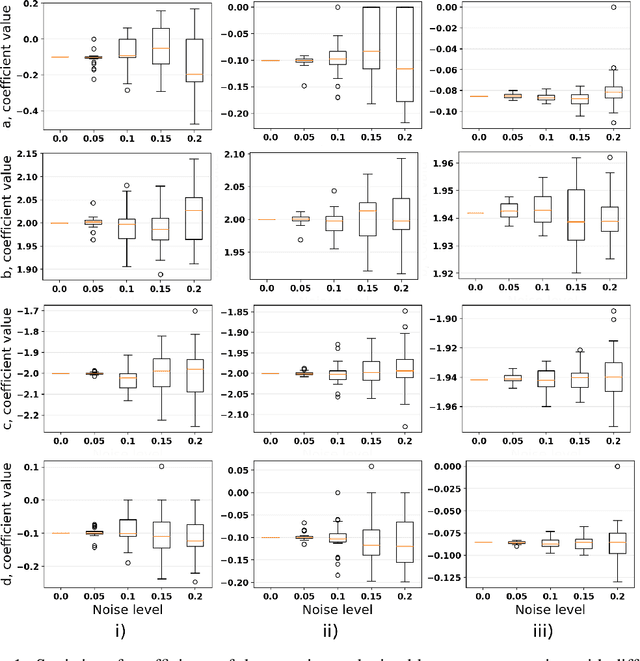
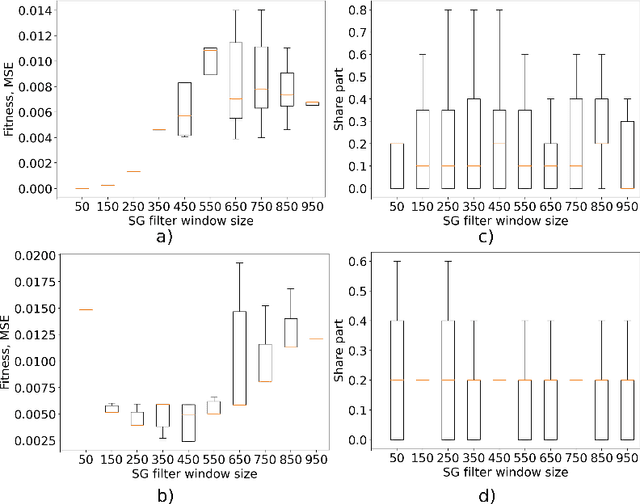
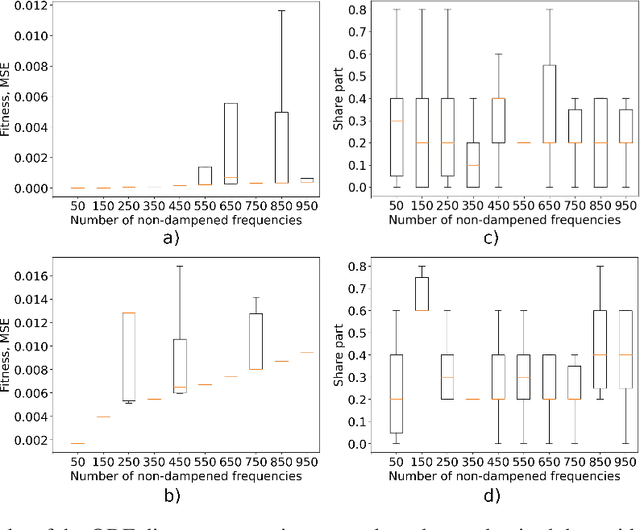
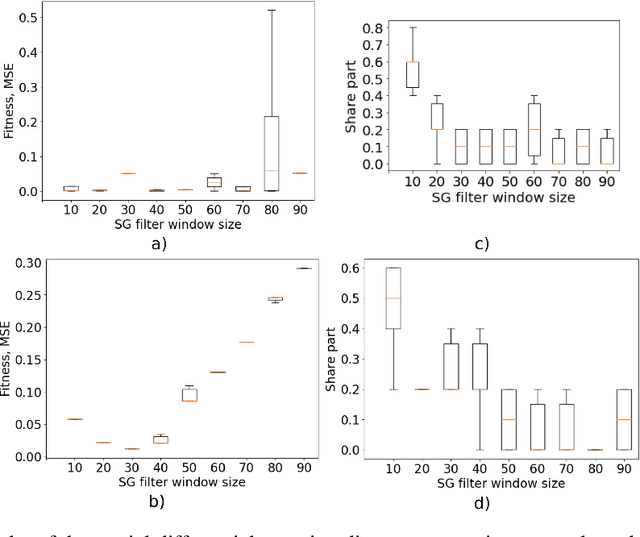
This paper explores the critical role of differentiation approaches for data-driven differential equation discovery. Accurate derivatives of the input data are essential for reliable algorithmic operation, particularly in real-world scenarios where measurement quality is inevitably compromised. We propose alternatives to the commonly used finite differences-based method, notorious for its instability in the presence of noise, which can exacerbate random errors in the data. Our analysis covers four distinct methods: Savitzky-Golay filtering, spectral differentiation, smoothing based on artificial neural networks, and the regularization of derivative variation. We evaluate these methods in terms of applicability to problems, similar to the real ones, and their ability to ensure the convergence of equation discovery algorithms, providing valuable insights for robust modeling of real-world processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge