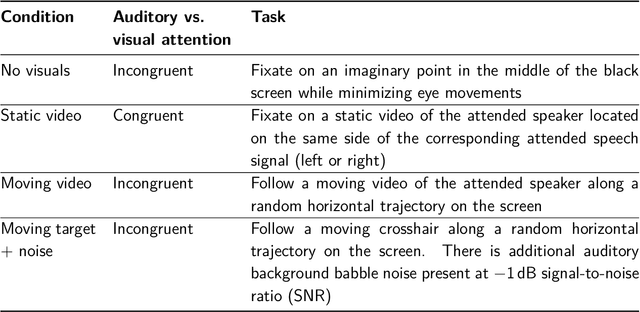
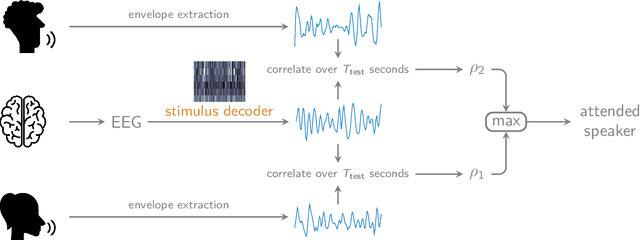
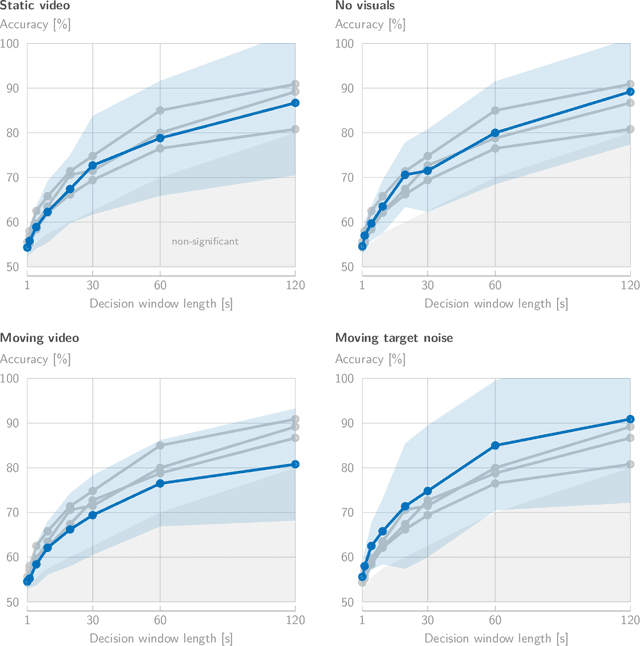
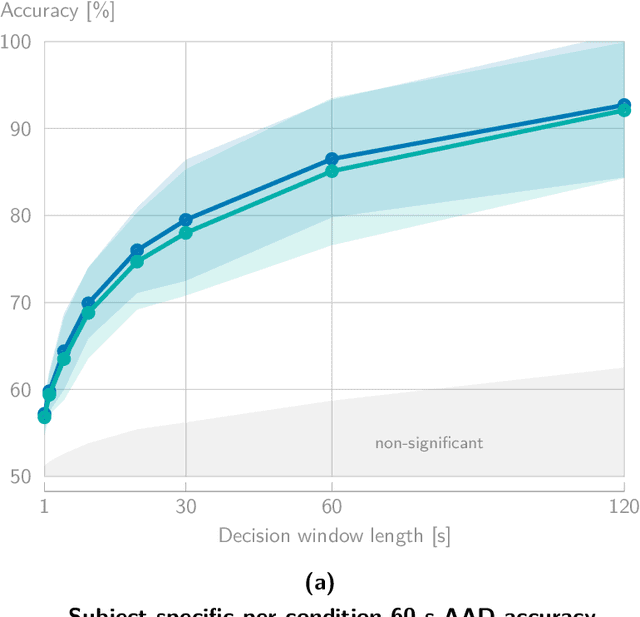
Linear stimulus reconstruction works on the KU Leuven audiovisual, gaze-controlled auditory attention decoding dataset

In a recent paper, we presented the KU Leuven audiovisual, gaze-controlled auditory attention decoding (AV-GC-AAD) dataset, in which we recorded electroencephalography (EEG) signals of participants attending to one out of two competing speakers under various audiovisual conditions. The main goal of this dataset was to disentangle the direction of gaze from the direction of auditory attention, in order to reveal gaze-related shortcuts in existing spatial AAD algorithms that aim to decode the (direction of) auditory attention directly from the EEG. Various methods based on spatial AAD do not achieve significant above-chance performances on our AV-GC-AAD dataset, indicating that previously reported results were mainly driven by eye gaze confounds in existing datasets. Still, these adverse outcomes are often discarded for reasons that are attributed to the limitations of the AV-GC-AAD dataset, such as the limited amount of data to train a working model, too much data heterogeneity due to different audiovisual conditions, or participants allegedly being unable to focus their auditory attention under the complex instructions. In this paper, we present the results of the linear stimulus reconstruction AAD algorithm and show that high AAD accuracy can be obtained within each individual condition and that the model generalizes across conditions, across new subjects, and even across datasets. Therefore, we eliminate any doubts that the inadequacy of the AV-GC-AAD dataset is the primary reason for the (spatial) AAD algorithms failing to achieve above-chance performance when compared to other datasets. Furthermore, this report provides a simple baseline evaluation procedure (including source code) that can serve as the minimal benchmark for all future AAD algorithms evaluated on this dataset.

Distributed Blind Source Separation based on FastICA

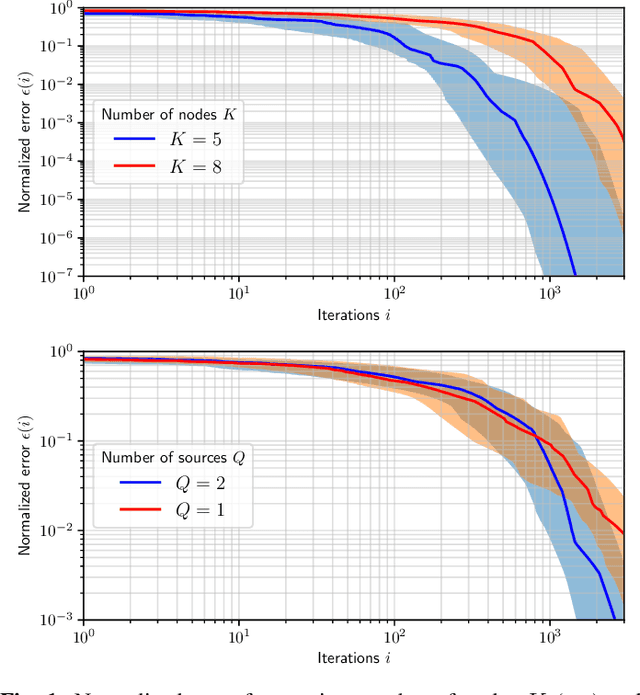
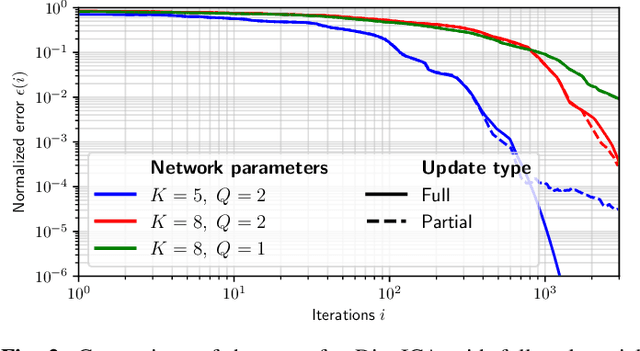
With the emergence of wireless sensor networks (WSNs), many traditional signal processing tasks are required to be computed in a distributed fashion, without transmissions of the raw data to a centralized processing unit, due to the limited energy and bandwidth resources available to the sensors. In this paper, we propose a distributed independent component analysis (ICA) algorithm, which aims at identifying the original signal sources based on observations of their mixtures measured at various sensor nodes. One of the most commonly used ICA algorithms is known as FastICA, which requires a spatial pre-whitening operation in the first step of the algorithm. Such a pre-whitening across all nodes of a WSN is impossible in a bandwidth-constrained distributed setting as it requires to correlate each channel with each other channel in the WSN. We show that an explicit network-wide pre-whitening step can be circumvented by leveraging the properties of the so-called Distributed Adaptive Signal Fusion (DASF) framework. Despite the lack of such a network-wide pre-whitening, we can still obtain the $Q$ least Gaussian independent components of the centralized ICA solution, where $Q$ scales linearly with the required communication load.

Conditional Gumbel-Softmax for constrained feature selection with application to node selection in wireless sensor networks

In this paper, we introduce Conditional Gumbel-Softmax as a method to perform end-to-end learning of the optimal feature subset for a given task and deep neural network (DNN) model, while adhering to certain pairwise constraints between the features. We do this by conditioning the selection of each feature in the subset on another feature. We demonstrate how this approach can be used to select the task-optimal nodes composing a wireless sensor network (WSN) while ensuring that none of the nodes that require communication between one another have too large of a distance between them, limiting the required power spent on this communication. We validate this approach on an emulated Wireless Electroencephalography (EEG) Sensor Network (WESN) solving a motor execution task. We analyze how the performance of the WESN varies as the constraints are made more stringent and how well the Conditional Gumbel-Softmax performs in comparison with a heuristic, greedy selection method. While the application focus of this paper is on wearable brain-computer interfaces, the proposed methodology is generic and can readily be applied to node deployment in wireless sensor networks and constrained feature selection in other applications as well.

Distributed Adaptive Spatial Filtering with Inexact Local Solvers

The Distributed Adaptive Signal Fusion (DASF) framework is a meta-algorithm for computing data-driven spatial filters in a distributed sensing platform with limited bandwidth and computational resources, such as a wireless sensor network. The convergence and optimality of the DASF algorithm has been extensively studied under the assumption that an exact, but possibly impractical solver for the local optimization problem at each updating node is available. In this work, we provide convergence and optimality results for the DASF framework when used with an inexact, finite-time solver such as (proximal) gradient descent or Newton's method. We provide sufficient conditions that the solver should satisfy in order to guarantee convergence of the resulting algorithm, and a lower bound for the convergence rate. We also provide numerical simulations to validate these theoretical results.

A Distributed Adaptive Algorithm for Non-Smooth Spatial Filtering Problems in Wireless Sensor Networks

A wireless sensor network often relies on a fusion center to process the data collected by each of its sensing nodes. Such an approach relies on the continuous transmission of raw data to the fusion center, which typically has a major impact on the sensors' battery life. To address this issue in the particular context of spatial filtering and signal fusion problems, we recently proposed the Distributed Adaptive Signal Fusion (DASF) algorithm, which distributively computes a spatial filter expressed as the solution of a smooth optimization problem involving the network-wide sensor signal statistics. In this work, we show that the DASF algorithm can be extended to compute the filters associated with a certain class of non-smooth optimization problems. This extension makes the addition of sparsity-inducing norms to the problem's cost function possible, allowing sensor selection to be performed in a distributed fashion, alongside the filtering task of interest, thereby further reducing the network's energy consumption. We provide a description of the algorithm, prove its convergence, and validate its performance and solution tracking capabilities with numerical experiments.

Stimulus-Informed Generalized Canonical Correlation Analysis for Group Analysis of Neural Responses

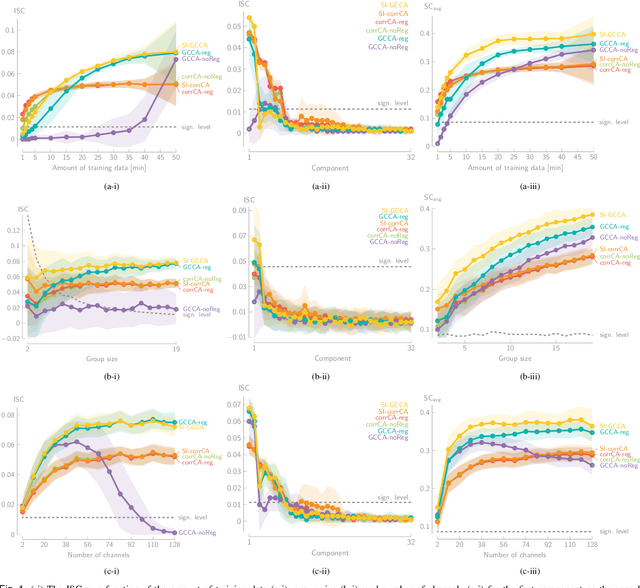
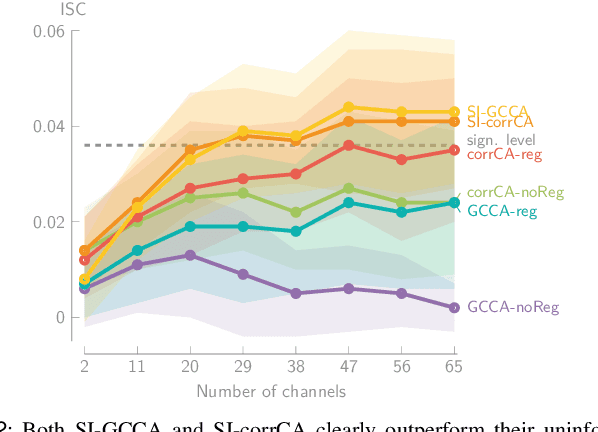
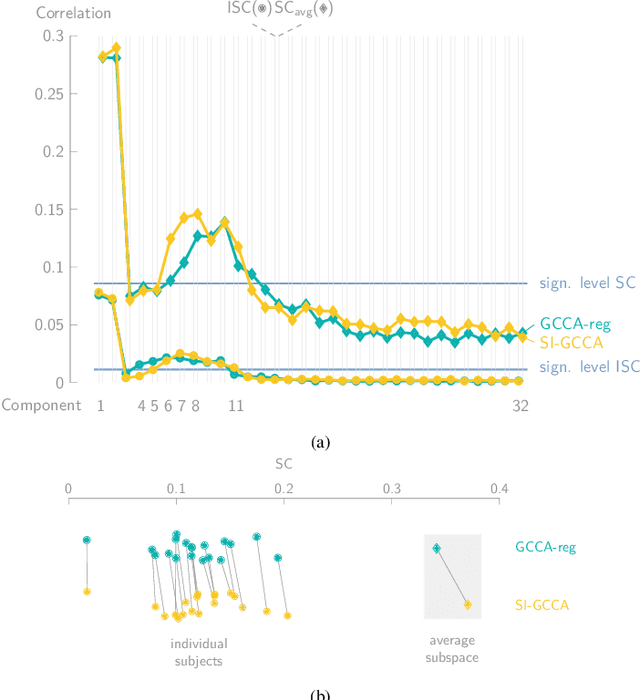
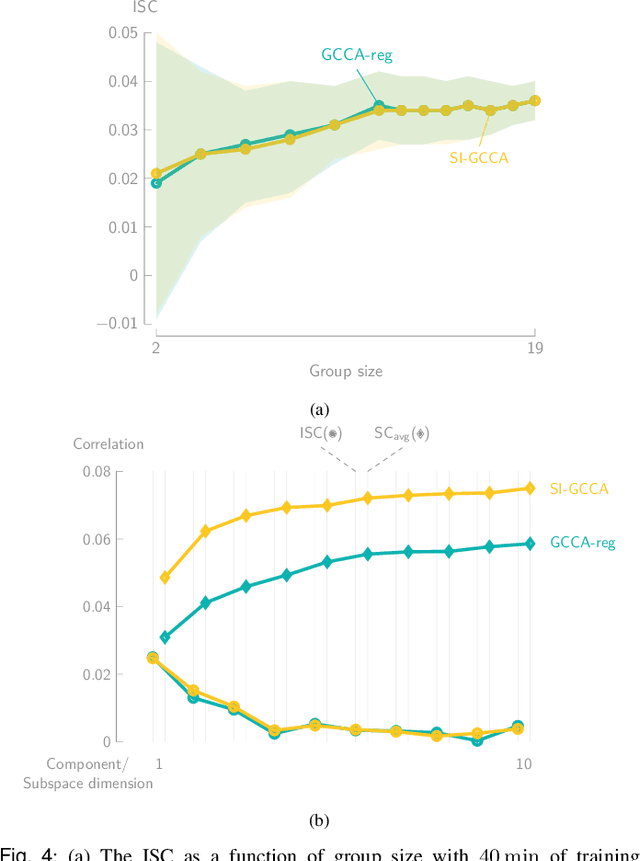
Various new brain-computer interface technologies or neuroscience applications require decoding stimulus-following neural responses to natural stimuli such as speech and video from, e.g., electroencephalography (EEG) signals. In this context, generalized canonical correlation analysis (GCCA) is often used as a group analysis technique, which allows the extraction of correlated signal components from the neural activity of multiple subjects attending to the same stimulus. GCCA can be used to improve the signal-to-noise ratio of the stimulus-following neural responses relative to all other irrelevant (non-)neural activity, or to quantify the correlated neural activity across multiple subjects in a group-wise coherence metric. However, the traditional GCCA technique is stimulus-unaware: no information about the stimulus is used to estimate the correlated components from the neural data of several subjects. Therefore, the GCCA technique might fail to extract relevant correlated signal components in practical situations where the amount of information is limited, for example, because of a limited amount of training data or group size. This motivates a new stimulus-informed GCCA (SI-GCCA) framework that allows taking the stimulus into account to extract the correlated components. We show that SI-GCCA outperforms GCCA in various practical settings, for both auditory and visual stimuli. Moreover, we showcase how SI-GCCA can be used to steer the estimation of the components towards the stimulus. As such, SI-GCCA substantially improves upon GCCA for various purposes, ranging from preprocessing to quantifying attention.

Minimally Informed Linear Discriminant Analysis: training an LDA model with unlabelled data

Linear Discriminant Analysis (LDA) is one of the oldest and most popular linear methods for supervised classification problems. In this paper, we demonstrate that it is possible to compute the exact projection vector from LDA models based on unlabelled data, if some minimal prior information is available. More precisely, we show that only one of the following three pieces of information is actually sufficient to compute the LDA projection vector if only unlabelled data are available: (1) the class average of one of the two classes, (2) the difference between both class averages (up to a scaling), or (3) the class covariance matrices (up to a scaling). These theoretical results are validated in numerical experiments, demonstrating that this minimally informed Linear Discriminant Analysis (MILDA) model closely matches the performance of a supervised LDA model. Furthermore, we show that the MILDA projection vector can be computed in a closed form with a computational cost comparable to LDA and is able to quickly adapt to non-stationary data, making it well-suited to use as an adaptive classifier.

Distributed Adaptive Signal Fusion for Fractional Programs

The distributed adaptive signal fusion (DASF) framework allows to solve spatial filtering optimization problems in a distributed and adaptive fashion over a bandwidth-constrained wireless sensor network. The DASF algorithm requires each node to sequentially build a compressed version of the original network-wide problem and solve it locally. However, these local problems can still result in a high computational load at the nodes, especially when the required solver is iterative. In this paper, we study the particular case of fractional programs, i.e., problems for which the objective function is a fraction of two continuous functions, which indeed require such iterative solvers. By exploiting the structure of a commonly used method for solving fractional programs and interleaving it with the iterations of the standard DASF algorithm, we obtain a distributed algorithm with a significantly reduced computational cost compared to the straightforward application of DASF as a meta-algorithm. We prove convergence and optimality of this "fractional DASF" (FDASF) algorithm and demonstrate its performance via numerical simulations.

A distributed neural network architecture for dynamic sensor selection with application to bandwidth-constrained body-sensor networks

We propose a dynamic sensor selection approach for deep neural networks (DNNs), which is able to derive an optimal sensor subset selection for each specific input sample instead of a fixed selection for the entire dataset. This dynamic selection is jointly learned with the task model in an end-to-end way, using the Gumbel-Softmax trick to allow the discrete decisions to be learned through standard backpropagation. We then show how we can use this dynamic selection to increase the lifetime of a wireless sensor network (WSN) by imposing constraints on how often each node is allowed to transmit. We further improve performance by including a dynamic spatial filter that makes the task-DNN more robust against the fact that it now needs to be able to handle a multitude of possible node subsets. Finally, we explain how the selection of the optimal channels can be distributed across the different nodes in a WSN. We validate this method on a use case in the context of body-sensor networks, where we use real electroencephalography (EEG) sensor data to emulate an EEG sensor network. We analyze the resulting trade-offs between transmission load and task accuracy.

A Distributed Adaptive Algorithm for Node-Specific Signal Fusion Problems in Wireless Sensor Networks

Wireless sensor networks consist of sensor nodes that are physically distributed over different locations. Spatial filtering procedures exploit the spatial correlation across these sensor signals to fuse them into a filtered signal satisfying some optimality condition. However, gathering the raw sensor data in a fusion center to solve the problem in a centralized way would lead to high energy and communication costs. The distributed adaptive signal fusion (DASF) framework has been proposed as a generic method to solve these signal fusion problems in a distributed fashion, which reduces the communication and energy costs in the network. The DASF framework assumes that there is a common goal across the nodes, i.e., the optimal filter is shared across the network. However, many applications require a node-specific objective, while all these node-specific objectives are still related via a common latent data model. In this work, we propose the DANSF algorithm which builds upon the DASF framework, and extends it to allow for node-specific spatial filtering problems.