Distributed Adaptive Spatial Filtering with Inexact Local Solvers

The Distributed Adaptive Signal Fusion (DASF) framework is a meta-algorithm for computing data-driven spatial filters in a distributed sensing platform with limited bandwidth and computational resources, such as a wireless sensor network. The convergence and optimality of the DASF algorithm has been extensively studied under the assumption that an exact, but possibly impractical solver for the local optimization problem at each updating node is available. In this work, we provide convergence and optimality results for the DASF framework when used with an inexact, finite-time solver such as (proximal) gradient descent or Newton's method. We provide sufficient conditions that the solver should satisfy in order to guarantee convergence of the resulting algorithm, and a lower bound for the convergence rate. We also provide numerical simulations to validate these theoretical results.

A Distributed Adaptive Algorithm for Non-Smooth Spatial Filtering Problems in Wireless Sensor Networks

A wireless sensor network often relies on a fusion center to process the data collected by each of its sensing nodes. Such an approach relies on the continuous transmission of raw data to the fusion center, which typically has a major impact on the sensors' battery life. To address this issue in the particular context of spatial filtering and signal fusion problems, we recently proposed the Distributed Adaptive Signal Fusion (DASF) algorithm, which distributively computes a spatial filter expressed as the solution of a smooth optimization problem involving the network-wide sensor signal statistics. In this work, we show that the DASF algorithm can be extended to compute the filters associated with a certain class of non-smooth optimization problems. This extension makes the addition of sparsity-inducing norms to the problem's cost function possible, allowing sensor selection to be performed in a distributed fashion, alongside the filtering task of interest, thereby further reducing the network's energy consumption. We provide a description of the algorithm, prove its convergence, and validate its performance and solution tracking capabilities with numerical experiments.

A Distributed Adaptive Algorithm for Non-Smooth Spatial Filtering Problems

Computing the optimal solution to a spatial filtering problems in a Wireless Sensor Network can incur large bandwidth and computational requirements if an approach relying on data centralization is used. The so-called distributed adaptive signal fusion (DASF) algorithm solves this problem by having the nodes collaboratively solve low-dimensional versions of the original optimization problem, relying solely on the exchange of compressed views of the sensor data between the nodes. However, the DASF algorithm has only been shown to converge for filtering problems that can be expressed as smooth optimization problems. In this paper, we explore an extension of the DASF algorithm to a family of non-smooth spatial filtering problems, allowing the addition of non-smooth regularizers to the optimization problem, which could for example be used to perform node selection, and eliminate nodes not contributing to the filter objective, therefore further reducing communication costs. We provide a convergence proof of the non-smooth DASF algorithm and validate its convergence via simulations in both a static and adaptive setting.

A Unified Algorithmic Framework for Distributed Adaptive Signal and Feature Fusion Problems -- Part II: Convergence Properties

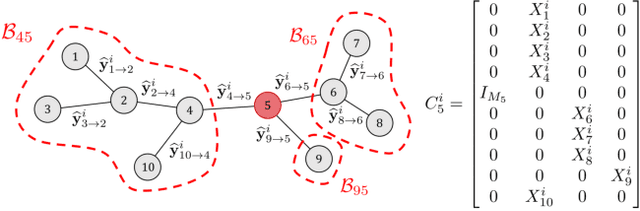
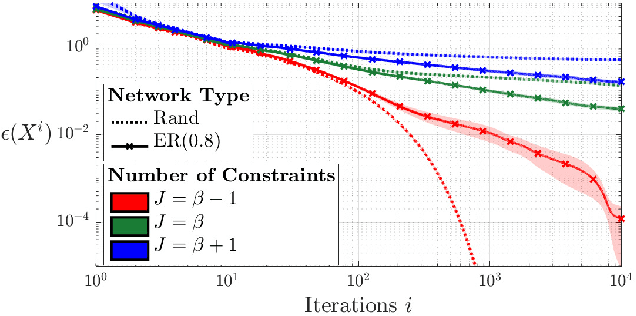
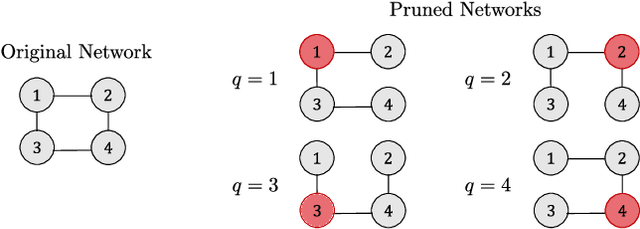
This paper studies the convergence conditions and properties of the distributed adaptive signal fusion (DASF) algorithm, the framework itself having been introduced in a `Part I' companion paper. The DASF algorithm can be used to solve linear signal and feature fusion optimization problems in a distributed fashion, and is in particular well-suited for solving spatial filtering optimization problems encountered in wireless sensor networks. The convergence results are provided along with rigorous proofs and analyses, as well as various example problems to which they apply. Additionally, we describe procedures that can be added to the DASF algorithm to ensure convergence in specific cases where some of the technical convergence conditions are not satisfied.