Distributed Blind Source Separation based on FastICA

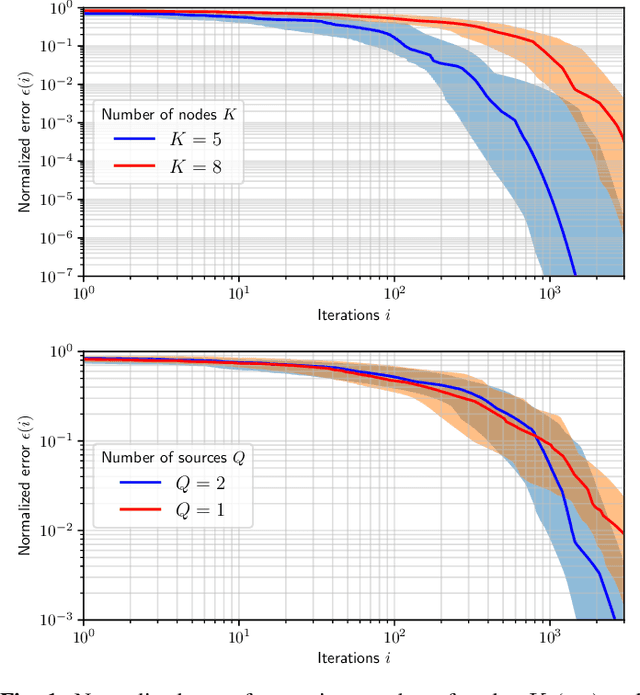
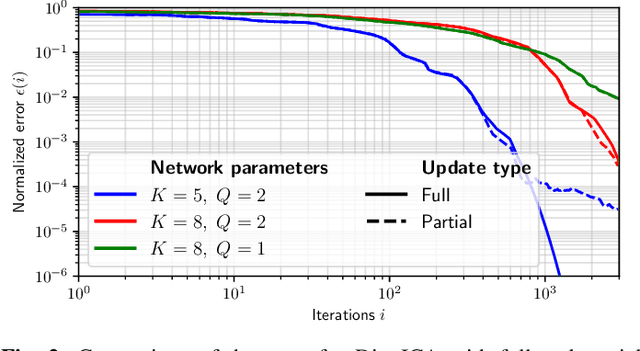
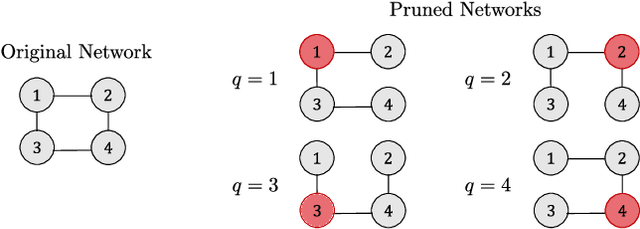
With the emergence of wireless sensor networks (WSNs), many traditional signal processing tasks are required to be computed in a distributed fashion, without transmissions of the raw data to a centralized processing unit, due to the limited energy and bandwidth resources available to the sensors. In this paper, we propose a distributed independent component analysis (ICA) algorithm, which aims at identifying the original signal sources based on observations of their mixtures measured at various sensor nodes. One of the most commonly used ICA algorithms is known as FastICA, which requires a spatial pre-whitening operation in the first step of the algorithm. Such a pre-whitening across all nodes of a WSN is impossible in a bandwidth-constrained distributed setting as it requires to correlate each channel with each other channel in the WSN. We show that an explicit network-wide pre-whitening step can be circumvented by leveraging the properties of the so-called Distributed Adaptive Signal Fusion (DASF) framework. Despite the lack of such a network-wide pre-whitening, we can still obtain the $Q$ least Gaussian independent components of the centralized ICA solution, where $Q$ scales linearly with the required communication load.

Distributed Adaptive Signal Fusion for Fractional Programs

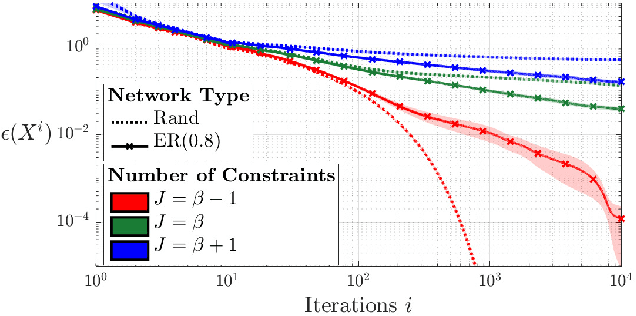
The distributed adaptive signal fusion (DASF) framework allows to solve spatial filtering optimization problems in a distributed and adaptive fashion over a bandwidth-constrained wireless sensor network. The DASF algorithm requires each node to sequentially build a compressed version of the original network-wide problem and solve it locally. However, these local problems can still result in a high computational load at the nodes, especially when the required solver is iterative. In this paper, we study the particular case of fractional programs, i.e., problems for which the objective function is a fraction of two continuous functions, which indeed require such iterative solvers. By exploiting the structure of a commonly used method for solving fractional programs and interleaving it with the iterations of the standard DASF algorithm, we obtain a distributed algorithm with a significantly reduced computational cost compared to the straightforward application of DASF as a meta-algorithm. We prove convergence and optimality of this "fractional DASF" (FDASF) algorithm and demonstrate its performance via numerical simulations.

A Distributed Adaptive Algorithm for Node-Specific Signal Fusion Problems in Wireless Sensor Networks

Wireless sensor networks consist of sensor nodes that are physically distributed over different locations. Spatial filtering procedures exploit the spatial correlation across these sensor signals to fuse them into a filtered signal satisfying some optimality condition. However, gathering the raw sensor data in a fusion center to solve the problem in a centralized way would lead to high energy and communication costs. The distributed adaptive signal fusion (DASF) framework has been proposed as a generic method to solve these signal fusion problems in a distributed fashion, which reduces the communication and energy costs in the network. The DASF framework assumes that there is a common goal across the nodes, i.e., the optimal filter is shared across the network. However, many applications require a node-specific objective, while all these node-specific objectives are still related via a common latent data model. In this work, we propose the DANSF algorithm which builds upon the DASF framework, and extends it to allow for node-specific spatial filtering problems.

A Unified Algorithmic Framework for Distributed Adaptive Signal and Feature Fusion Problems -- Part II: Convergence Properties

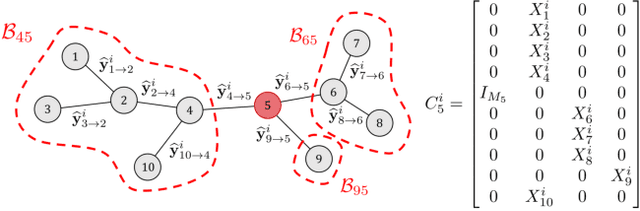
This paper studies the convergence conditions and properties of the distributed adaptive signal fusion (DASF) algorithm, the framework itself having been introduced in a `Part I' companion paper. The DASF algorithm can be used to solve linear signal and feature fusion optimization problems in a distributed fashion, and is in particular well-suited for solving spatial filtering optimization problems encountered in wireless sensor networks. The convergence results are provided along with rigorous proofs and analyses, as well as various example problems to which they apply. Additionally, we describe procedures that can be added to the DASF algorithm to ensure convergence in specific cases where some of the technical convergence conditions are not satisfied.

A Unified Algorithmic Framework for Distributed Adaptive Signal and Feature Fusion Problems -- Part I: Algorithm Derivation

In this paper, we describe a general algorithmic framework for solving linear signal or feature fusion optimization problems in a distributed setting, for example in a wireless sensor network (WSN). These problems require linearly combining the observed signals (or features thereof) collected at the various sensor nodes to satisfy a pre-defined optimization criterion. The framework covers several classical spatial filtering problems, including minimum variance beamformers, multi-channel Wiener filters, principal component analysis, canonical correlation analysis, (generalized) eigenvalue problems, etc. The proposed distributed adaptive signal fusion (DASF) algorithm is an iterative method which solves these types of problems by letting each node share a linearly compressed version of the local sensor signal observations with its neighbors to reduce the energy and bandwidth requirements of the network. We first discuss the case of fully-connected networks and then extend the analysis to more general network topologies. The general DASF algorithm is shown to have several existing distributed algorithms from the literature as a special case, while at the same time allowing to solve new distributed problems as well with guaranteed convergence and optimality. This paper focuses on the algorithm derivation of the DASF framework along with simulations demonstrating its performance. A technical analysis along with convergence conditions and proofs are provided in a companion paper.