CT-NOR: Representing and Reasoning About Events in Continuous Time

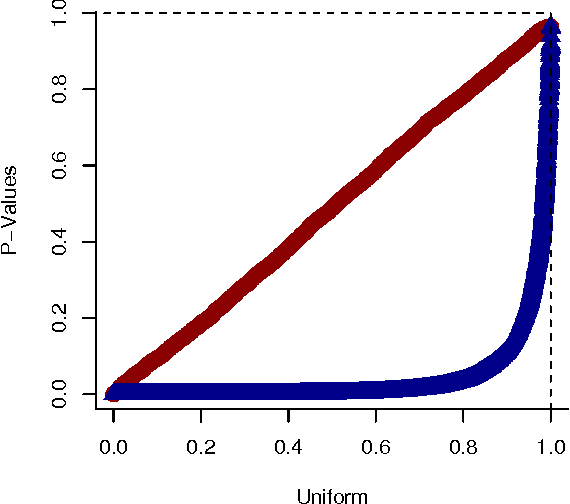
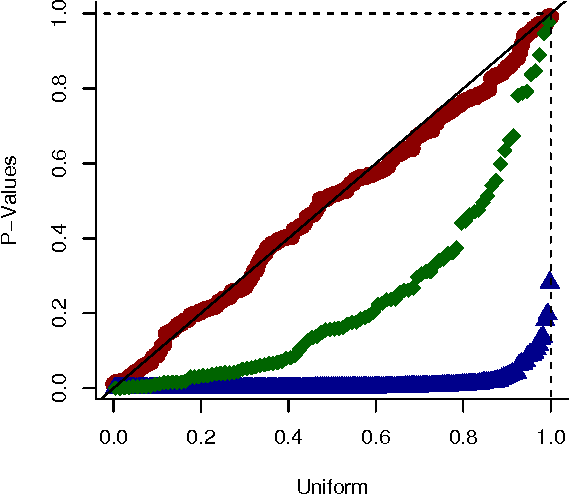
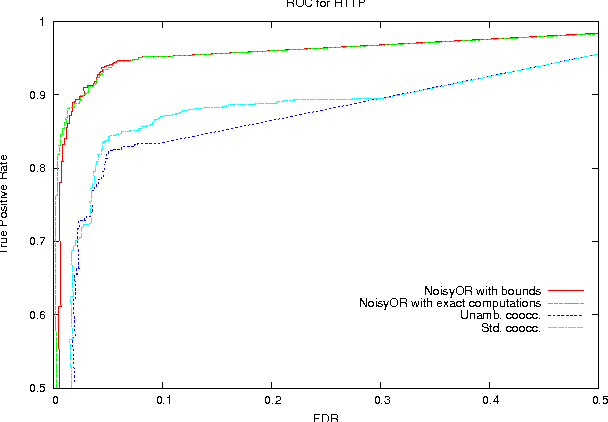
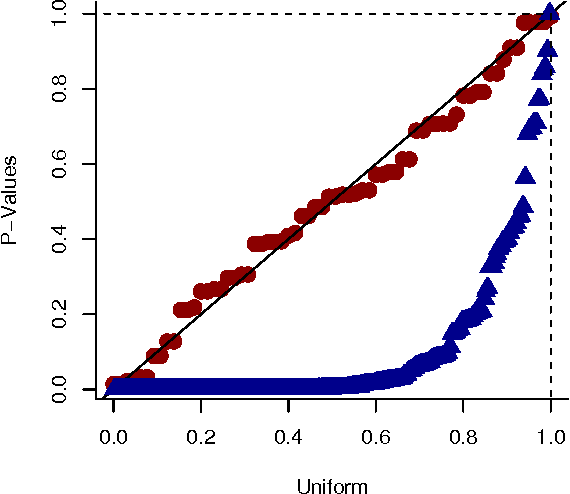
We present a generative model for representing and reasoning about the relationships among events in continuous time. We apply the model to the domain of networked and distributed computing environments where we fit the parameters of the model from timestamp observations, and then use hypothesis testing to discover dependencies between the events and changes in behavior for monitoring and diagnosis. After introducing the model, we present an EM algorithm for fitting the parameters and then present the hypothesis testing approach for both dependence discovery and change-point detection. We validate the approach for both tasks using real data from a trace of network events at Microsoft Research Cambridge. Finally, we formalize the relationship between the proposed model and the noisy-or gate for cases when time can be discretized.

Modeling Events with Cascades of Poisson Processes

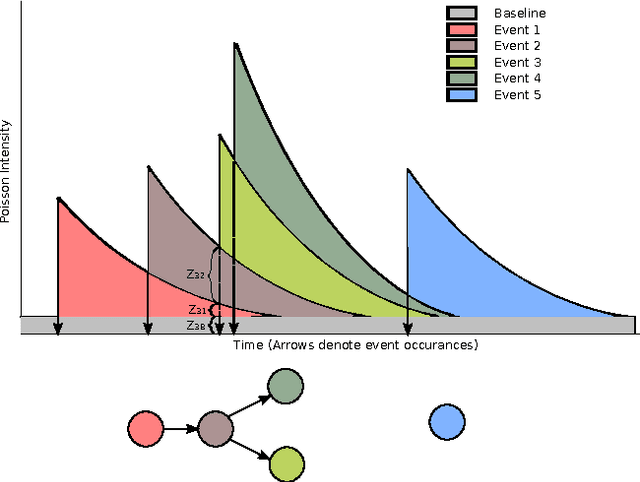
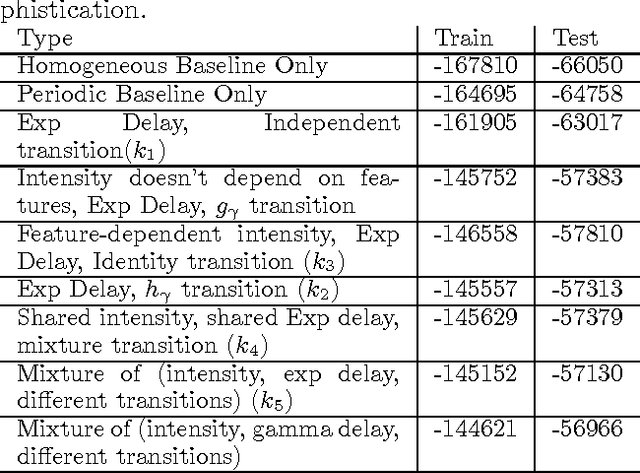
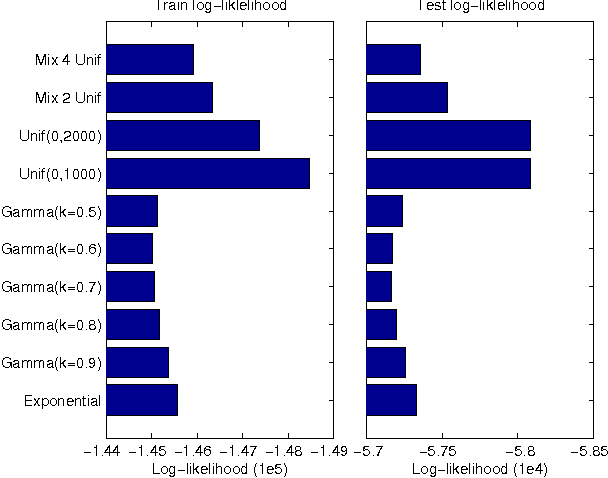
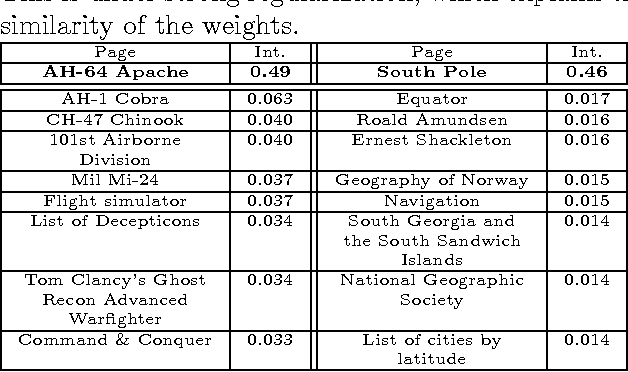
We present a probabilistic model of events in continuous time in which each event triggers a Poisson process of successor events. The ensemble of observed events is thereby modeled as a superposition of Poisson processes. Efficient inference is feasible under this model with an EM algorithm. Moreover, the EM algorithm can be implemented as a distributed algorithm, permitting the model to be applied to very large datasets. We apply these techniques to the modeling of Twitter messages and the revision history of Wikipedia.

On the Stability of Empirical Risk Minimization in the Presence of Multiple Risk Minimizers

Recently Kutin and Niyogi investigated several notions of algorithmic stability--a property of a learning map conceptually similar to continuity--showing that training-stability is sufficient for consistency of Empirical Risk Minimization while distribution-free CV-stability is necessary and sufficient for having finite VC-dimension. This paper concerns a phase transition in the training stability of ERM, conjectured by the same authors. Kutin and Niyogi proved that ERM on finite hypothesis spaces containing a unique risk minimizer has training stability that scales exponentially with sample size, and conjectured that the existence of multiple risk minimizers prevents even super-quadratic convergence. We prove this result for the strictly weaker notion of CV-stability, positively resolving the conjecture.