Stable Differentiable Modal Synthesis for Learning Nonlinear Dynamics

Modal methods are a long-standing approach to physical modelling synthesis. Extensions to nonlinear problems are possible, including the case of a high-amplitude vibration of a string. A modal decomposition leads to a densely coupled nonlinear system of ordinary differential equations. Recent work in scalar auxiliary variable techniques has enabled construction of explicit and stable numerical solvers for such classes of nonlinear systems. On the other hand, machine learning approaches (in particular neural ordinary differential equations) have been successful in modelling nonlinear systems automatically from data. In this work, we examine how scalar auxiliary variable techniques can be combined with neural ordinary differential equations to yield a stable differentiable model capable of learning nonlinear dynamics. The proposed approach leverages the analytical solution for linear vibration of system's modes so that physical parameters of a system remain easily accessible after the training without the need for a parameter encoder in the model architecture. As a proof of concept, we generate synthetic data for the nonlinear transverse vibration of a string and show that the model can be trained to reproduce the nonlinear dynamics of the system. Sound examples are presented.

Gradient-based Optimisation of Modulation Effects

Modulation effects such as phasers, flangers and chorus effects are heavily used in conjunction with the electric guitar. Machine learning based emulation of analog modulation units has been investigated in recent years, but most methods have either been limited to one class of effect or suffer from a high computational cost or latency compared to canonical digital implementations. Here, we build on previous work and present a framework for modelling flanger, chorus and phaser effects based on differentiable digital signal processing. The model is trained in the time-frequency domain, but at inference operates in the time-domain, requiring zero latency. We investigate the challenges associated with gradient-based optimisation of such effects, and show that low-frequency weighting of loss functions avoids convergence to local minima when learning delay times. We show that when trained against analog effects units, sound output from the model is in some cases perceptually indistinguishable from the reference, but challenges still remain for effects with long delay times and feedback.

Anti-aliasing of neural distortion effects via model fine tuning

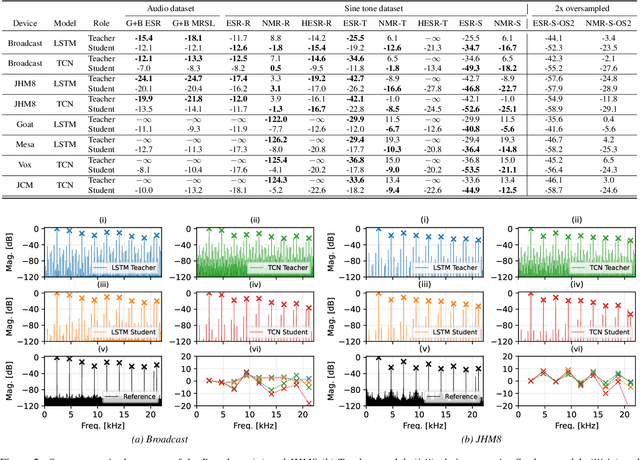
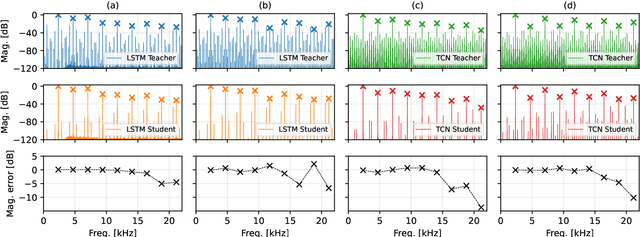
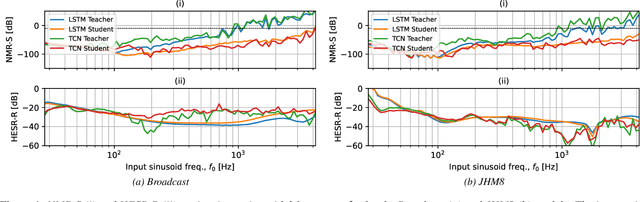
Neural networks have become ubiquitous with guitar distortion effects modelling in recent years. Despite their ability to yield perceptually convincing models, they are susceptible to frequency aliasing when driven by high frequency and high gain inputs. Nonlinear activation functions create both the desired harmonic distortion and unwanted aliasing distortion as the bandwidth of the signal is expanded beyond the Nyquist frequency. Here, we present a method for reducing aliasing in neural models via a teacher-student fine tuning approach, where the teacher is a pre-trained model with its weights frozen, and the student is a copy of this with learnable parameters. The student is fine-tuned against an aliasing-free dataset generated by passing sinusoids through the original model and removing non-harmonic components from the output spectra. Our results show that this method significantly suppresses aliasing for both long-short-term-memory networks (LSTM) and temporal convolutional networks (TCN). In the majority of our case studies, the reduction in aliasing was greater than that achieved by two times oversampling. One side-effect of the proposed method is that harmonic distortion components are also affected. This adverse effect was found to be model-dependent, with the LSTM models giving the best balance between anti-aliasing and preserving the perceived similarity to an analog reference device.

Learning Nonlinear Dynamics in Physical Modelling Synthesis using Neural Ordinary Differential Equations

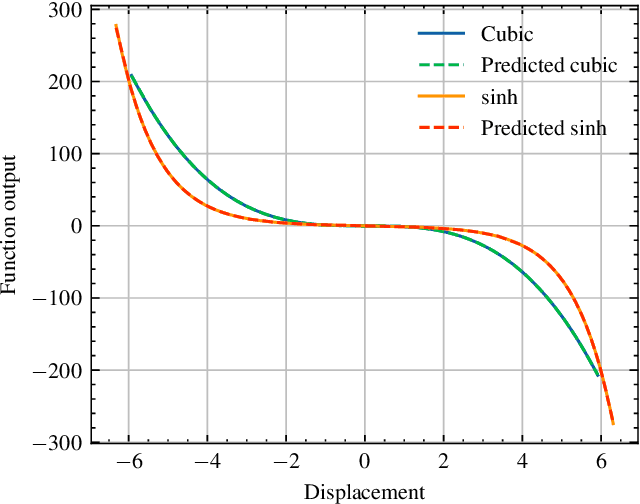
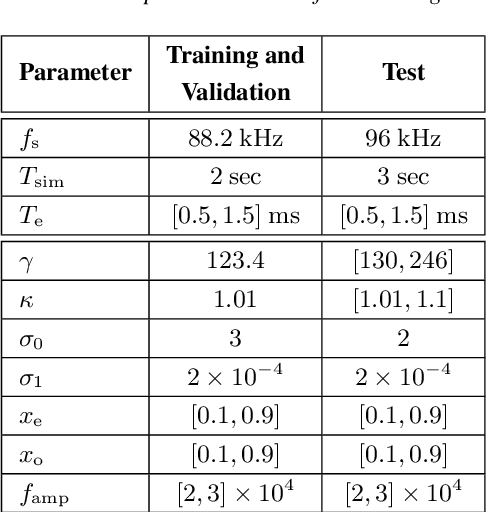
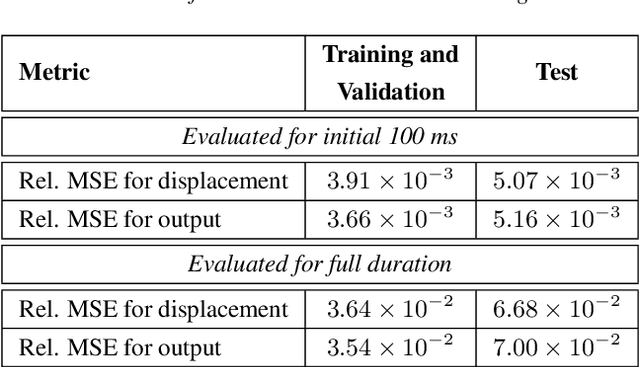
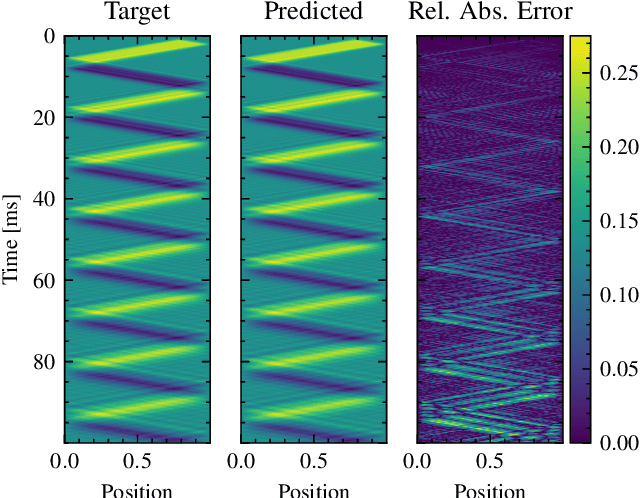
Modal synthesis methods are a long-standing approach for modelling distributed musical systems. In some cases extensions are possible in order to handle geometric nonlinearities. One such case is the high-amplitude vibration of a string, where geometric nonlinear effects lead to perceptually important effects including pitch glides and a dependence of brightness on striking amplitude. A modal decomposition leads to a coupled nonlinear system of ordinary differential equations. Recent work in applied machine learning approaches (in particular neural ordinary differential equations) has been used to model lumped dynamic systems such as electronic circuits automatically from data. In this work, we examine how modal decomposition can be combined with neural ordinary differential equations for modelling distributed musical systems. The proposed model leverages the analytical solution for linear vibration of system's modes and employs a neural network to account for nonlinear dynamic behaviour. Physical parameters of a system remain easily accessible after the training without the need for a parameter encoder in the network architecture. As an initial proof of concept, we generate synthetic data for a nonlinear transverse string and show that the model can be trained to reproduce the nonlinear dynamics of the system. Sound examples are presented.

Unsupervised Estimation of Nonlinear Audio Effects: Comparing Diffusion-Based and Adversarial approaches

Accurately estimating nonlinear audio effects without access to paired input-output signals remains a challenging problem.This work studies unsupervised probabilistic approaches for solving this task. We introduce a method, novel for this application, based on diffusion generative models for blind system identification, enabling the estimation of unknown nonlinear effects using black- and gray-box models. This study compares this method with a previously proposed adversarial approach, analyzing the performance of both methods under different parameterizations of the effect operator and varying lengths of available effected recordings.Through experiments on guitar distortion effects, we show that the diffusion-based approach provides more stable results and is less sensitive to data availability, while the adversarial approach is superior at estimating more pronounced distortion effects. Our findings contribute to the robust unsupervised blind estimation of audio effects, demonstrating the potential of diffusion models for system identification in music technology.

Resampling Filter Design for Multirate Neural Audio Effect Processing

Neural networks have become ubiquitous in audio effects modelling, especially for guitar amplifiers and distortion pedals. One limitation of such models is that the sample rate of the training data is implicitly encoded in the model weights and therefore not readily adjustable at inference. Recent work explored modifications to recurrent neural network architecture to approximate a sample rate independent system, enabling audio processing at a rate that differs from the original training rate. This method works well for integer oversampling and can reduce aliasing caused by nonlinear activation functions. For small fractional changes in sample rate, fractional delay filters can be used to approximate sample rate independence, but in some cases this method fails entirely. Here, we explore the use of signal resampling at the input and output of the neural network as an alternative solution. We investigate several resampling filter designs and show that a two-stage design consisting of a half-band IIR filter cascaded with a Kaiser window FIR filter can give similar or better results to the previously proposed model adjustment method with many fewer operations per sample and less than one millisecond of latency at typical audio rates. Furthermore, we investigate interpolation and decimation filters for the task of integer oversampling and show that cascaded half-band IIR and FIR designs can be used in conjunction with the model adjustment method to reduce aliasing in a range of distortion effect models.

Estimation and Restoration of Unknown Nonlinear Distortion using Diffusion

The restoration of nonlinearly distorted audio signals, alongside the identification of the applied memoryless nonlinear operation, is studied. The paper focuses on the difficult but practically important case in which both the nonlinearity and the original input signal are unknown. The proposed method uses a generative diffusion model trained unconditionally on guitar or speech signals to jointly model and invert the nonlinear system at inference time. Both the memoryless nonlinear function model and the restored audio signal are obtained as output. Successful example case studies are presented including inversion of hard and soft clipping, digital quantization, half-wave rectification, and wavefolding nonlinearities. Our results suggest that, out of the nonlinear functions tested here, the cubic Catmull-Rom spline is best suited to approximating these nonlinearities. In the case of guitar recordings, comparisons with informed and supervised methods show that the proposed blind method is at least as good as they are in terms of objective metrics. Experiments on distorted speech show that the proposed blind method outperforms general-purpose speech enhancement techniques and restores the original voice quality. The proposed method can be applied to audio effects modeling, restoration of music and speech recordings, and characterization of analog recording media.

Open-Amp: Synthetic Data Framework for Audio Effect Foundation Models

This paper introduces Open-Amp, a synthetic data framework for generating large-scale and diverse audio effects data. Audio effects are relevant to many musical audio processing and Music Information Retrieval (MIR) tasks, such as modelling of analog audio effects, automatic mixing, tone matching and transcription. Existing audio effects datasets are limited in scope, usually including relatively few audio effects processors and a limited amount of input audio signals. Our proposed framework overcomes these issues, by crowdsourcing neural network emulations of guitar amplifiers and effects, created by users of open-source audio effects emulation software. This allows users of Open-Amp complete control over the input signals to be processed by the effects models, as well as providing high-quality emulations of hundreds of devices. Open-Amp can render audio online during training, allowing great flexibility in data augmentation. Our experiments show that using Open-Amp to train a guitar effects encoder achieves new state-of-the-art results on multiple guitar effects classification tasks. Furthermore, we train a one-to-many guitar effects model using Open-Amp, and use it to emulate unseen analog effects via manipulation of its learned latent space, indicating transferability to analog guitar effects data.

Interpolation filter design for sample rate independent audio effect RNNs

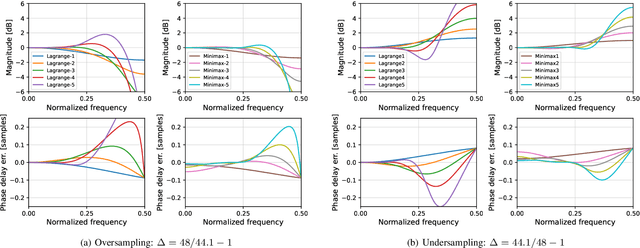
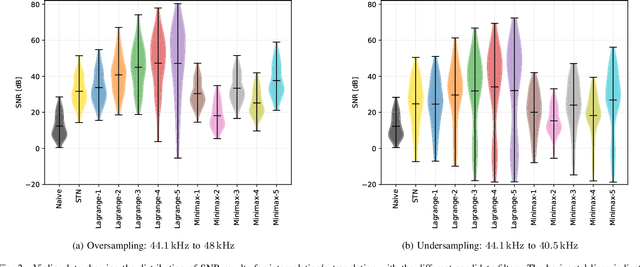
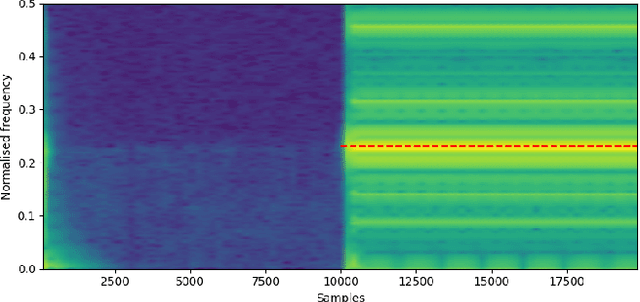
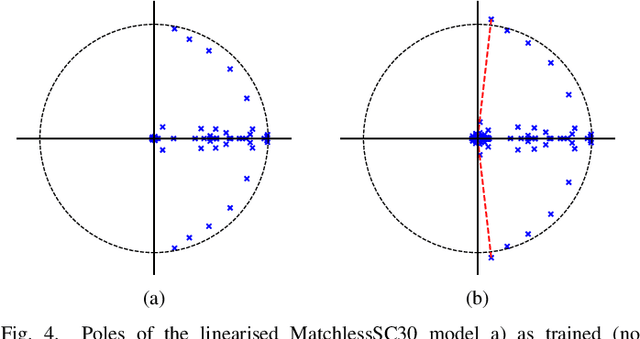
Recurrent neural networks (RNNs) are effective at emulating the non-linear, stateful behavior of analog guitar amplifiers and distortion effects. Unlike the case of direct circuit simulation, RNNs have a fixed sample rate encoded in their model weights, making the sample rate non-adjustable during inference. Recent work has proposed increasing the sample rate of RNNs at inference (oversampling) by increasing the feedback delay length in samples, using a fractional delay filter for non-integer conversions. Here, we investigate the task of lowering the sample rate at inference (undersampling), and propose using an extrapolation filter to approximate the required fractional signal advance. We consider two filter design methods and analyze the impact of filter order on audio quality. Our results show that the correct choice of filter can give high quality results for both oversampling and undersampling; however, in some cases the sample rate adjustment leads to unwanted artefacts in the output signal. We analyse these failure cases through linearised stability analysis, showing that they result from instability around a fixed point. This approach enables an informed prediction of suitable interpolation filters for a given RNN model before runtime.

Sample Rate Independent Recurrent Neural Networks for Audio Effects Processing

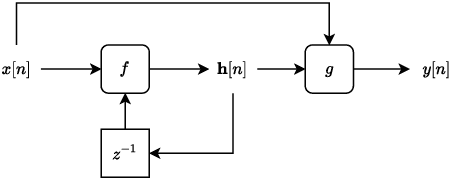
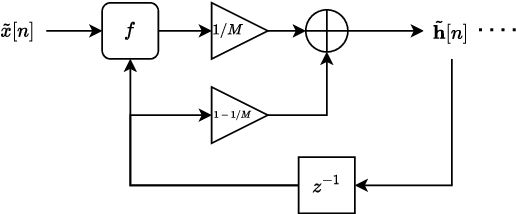
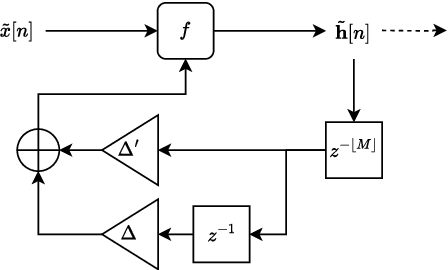
In recent years, machine learning approaches to modelling guitar amplifiers and effects pedals have been widely investigated and have become standard practice in some consumer products. In particular, recurrent neural networks (RNNs) are a popular choice for modelling non-linear devices such as vacuum tube amplifiers and distortion circuitry. One limitation of such models is that they are trained on audio at a specific sample rate and therefore give unreliable results when operating at another rate. Here, we investigate several methods of modifying RNN structures to make them approximately sample rate independent, with a focus on oversampling. In the case of integer oversampling, we demonstrate that a previously proposed delay-based approach provides high fidelity sample rate conversion whilst additionally reducing aliasing. For non-integer sample rate adjustment, we propose two novel methods and show that one of these, based on cubic Lagrange interpolation of a delay-line, provides a significant improvement over existing methods. To our knowledge, this work provides the first in-depth study into this problem.