Theoretically Grounded Pruning of Large Ground Sets for Constrained, Discrete Optimization

Modern instances of combinatorial optimization problems often exhibit billion-scale ground sets, which have many uninformative or redundant elements. In this work, we develop light-weight pruning algorithms to quickly discard elements that are unlikely to be part of an optimal solution. Under mild assumptions on the instance, we prove theoretical guarantees on the fraction of the optimal value retained and the size of the resulting pruned ground set. Through extensive experiments on real-world datasets for various applications, we demonstrate that our algorithm, QuickPrune, efficiently prunes over 90% of the ground set and outperforms state-of-the-art classical and machine learning heuristics for pruning.

A Benchmark for Maximum Cut: Towards Standardization of the Evaluation of Learned Heuristics for Combinatorial Optimization

Recently, there has been much work on the design of general heuristics for graph-based, combinatorial optimization problems via the incorporation of Graph Neural Networks (GNNs) to learn distribution-specific solution structures.However, there is a lack of consistency in the evaluation of these heuristics, in terms of the baselines and instances chosen, which makes it difficult to assess the relative performance of the algorithms. In this paper, we propose an open-source benchmark suite MaxCut-Bench dedicated to the NP-hard Maximum Cut problem in both its weighted and unweighted variants, based on a careful selection of instances curated from diverse graph datasets. The suite offers a unified interface to various heuristics, both traditional and machine learning-based. Next, we use the benchmark in an attempt to systematically corroborate or reproduce the results of several, popular learning-based approaches, including S2V-DQN [31], ECO-DQN [4], among others, in terms of three dimensions: objective value, generalization, and scalability. Our empirical results show that several of the learned heuristics fail to outperform a naive greedy algorithm, and that only one of them consistently outperforms Tabu Search, a simple, general heuristic based upon local search. Furthermore, we find that the performance of ECO-DQN remains the same or is improved if the GNN is replaced by a simple linear regression on a subset of the features that are related to Tabu Search. Code, data, and pretrained models are available at: \url{https://github.com/ankurnath/MaxCut-Bench}.

Guided Combinatorial Algorithms for Submodular Maximization

For constrained, not necessarily monotone submodular maximization, guiding the measured continuous greedy algorithm with a local search algorithm currently obtains the state-of-the-art approximation factor of 0.401 \citep{buchbinder2023constrained}. These algorithms rely upon the multilinear extension and the Lovasz extension of a submodular set function. However, the state-of-the-art approximation factor of combinatorial algorithms has remained $1/e \approx 0.367$ \citep{buchbinder2014submodular}. In this work, we develop combinatorial analogues of the guided measured continuous greedy algorithm and obtain approximation ratio of $0.385$ in $\oh{ kn }$ queries to the submodular set function for size constraint, and $0.305$ for a general matroid constraint. Further, we derandomize these algorithms, maintaining the same ratio and asymptotic time complexity. Finally, we develop a deterministic, nearly linear time algorithm with ratio $0.377$.

Unveiling the Limits of Learned Local Search Heuristics: Are You the Mightiest of the Meek?

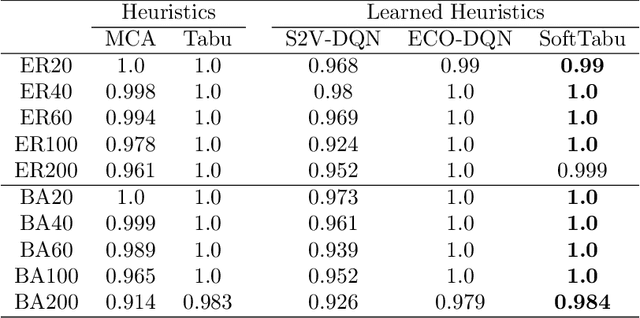
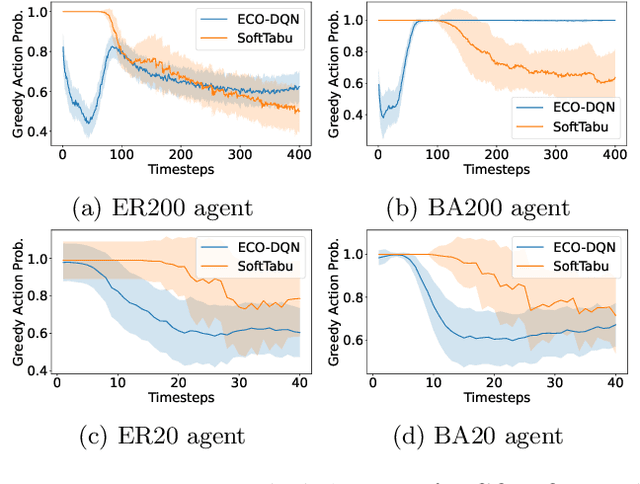
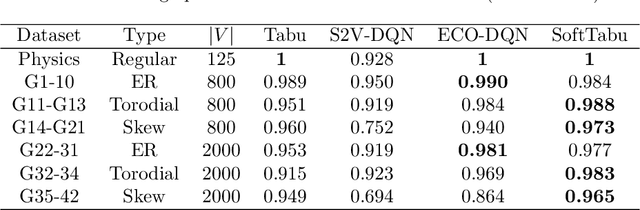
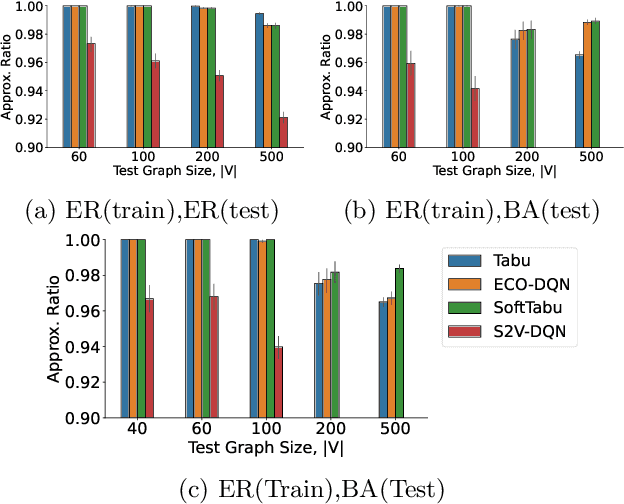
In recent years, combining neural networks with local search heuristics has become popular in the field of combinatorial optimization. Despite its considerable computational demands, this approach has exhibited promising outcomes with minimal manual engineering. However, we have identified three critical limitations in the empirical evaluation of these integration attempts. Firstly, instances with moderate complexity and weak baselines pose a challenge in accurately evaluating the effectiveness of learning-based approaches. Secondly, the absence of an ablation study makes it difficult to quantify and attribute improvements accurately to the deep learning architecture. Lastly, the generalization of learned heuristics across diverse distributions remains underexplored. In this study, we conduct a comprehensive investigation into these identified limitations. Surprisingly, we demonstrate that a simple learned heuristic based on Tabu Search surpasses state-of-the-art (SOTA) learned heuristics in terms of performance and generalizability. Our findings challenge prevailing assumptions and open up exciting avenues for future research and innovation in combinatorial optimization.

RELS-DQN: A Robust and Efficient Local Search Framework for Combinatorial Optimization

Combinatorial optimization (CO) aims to efficiently find the best solution to NP-hard problems ranging from statistical physics to social media marketing. A wide range of CO applications can benefit from local search methods because they allow reversible action over greedy policies. Deep Q-learning (DQN) using message-passing neural networks (MPNN) has shown promise in replicating the local search behavior and obtaining comparable results to the local search algorithms. However, the over-smoothing and the information loss during the iterations of message passing limit its robustness across applications, and the large message vectors result in memory inefficiency. Our paper introduces RELS-DQN, a lightweight DQN framework that exhibits the local search behavior while providing practical scalability. Using the RELS-DQN model trained on one application, it can generalize to various applications by providing solution values higher than or equal to both the local search algorithms and the existing DQN models while remaining efficient in runtime and memory.

Learning Strategic Value and Cooperation in Multi-Player Stochastic Games through Side Payments

For general-sum, n-player, strategic games with transferable utility, the Harsanyi-Shapley value provides a computable method to both 1) quantify the strategic value of a player; and 2) make cooperation rational through side payments. We give a simple formula to compute the HS value in normal-form games. Next, we provide two methods to generalize the HS values to stochastic (or Markov) games, and show that one of them may be computed using generalized Q-learning algorithms. Finally, an empirical validation is performed on stochastic grid-games with three or more players. Source code is provided to compute HS values for both the normal-form and stochastic game setting.

DASH: Distributed Adaptive Sequencing Heuristic for Submodular Maximization

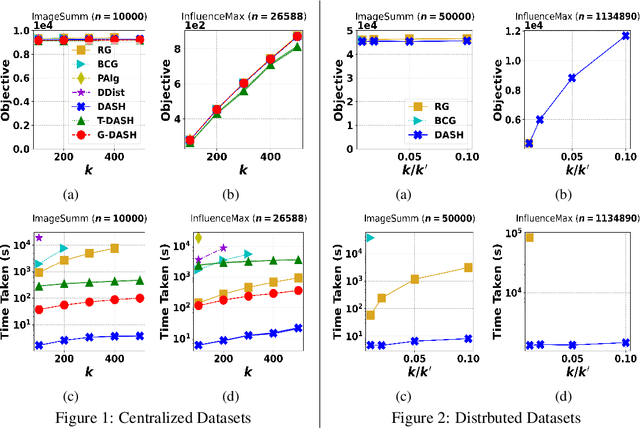
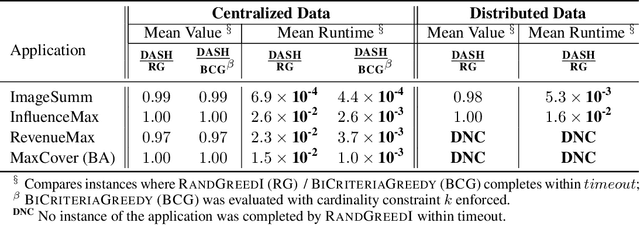
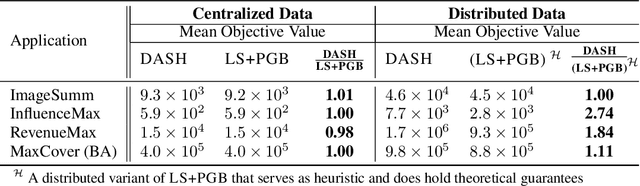
The development of parallelizable algorithms for monotone, submodular maximization subject to cardinality constraint (SMCC) has resulted in two separate research directions: centralized algorithms with low adaptive complexity, which require random access to the entire dataset; and distributed MapReduce (MR) model algorithms, that use a small number of MR rounds of computation. Currently, no MR model algorithm is known to use sublinear number of adaptive rounds which limits their practical performance. We study the SMCC problem in a distributed setting and present three separate MR model algorithms that introduce sublinear adaptivity in a distributed setup. Our primary algorithm, DASH achieves an approximation of $\frac{1}{2}(1-1/e-\varepsilon)$ using one MR round, while its multi-round variant METADASH enables MR model algorithms to be run on large cardinality constraints that were previously not possible. The two additional algorithms, T-DASH and G-DASH provide an improved ratio of ($\frac{3}{8}-\varepsilon$) and ($1-1/e-\varepsilon$) respectively using one and $(1/\varepsilon)$ MR rounds . All our proposed algorithms have sublinear adaptive complexity and we provide extensive empirical evidence to establish: DASH is orders of magnitude faster than the state-of-the-art distributed algorithms while producing nearly identical solution values; and validate the versatility of DASH in obtaining feasible solutions on both centralized and distributed data.

Best of Both Worlds: Practical and Theoretically Optimal Submodular Maximization in Parallel

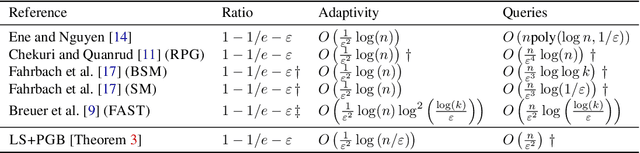
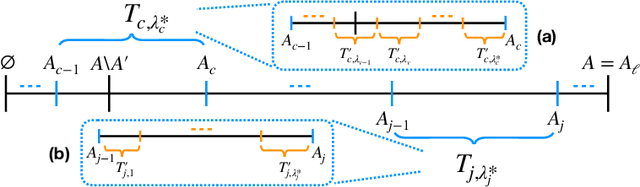
For the problem of maximizing a monotone, submodular function with respect to a cardinality constraint $k$ on a ground set of size $n$, we provide an algorithm that achieves the state-of-the-art in both its empirical performance and its theoretical properties, in terms of adaptive complexity, query complexity, and approximation ratio; that is, it obtains, with high probability, query complexity of $O(n)$ in expectation, adaptivity of $O(\log(n))$, and approximation ratio of nearly $1-1/e$. The main algorithm is assembled from two components which may be of independent interest. The first component of our algorithm, LINEARSEQ, is useful as a preprocessing algorithm to improve the query complexity of many algorithms. Moreover, a variant of LINEARSEQ is shown to have adaptive complexity of $O( \log (n / k) )$ which is smaller than that of any previous algorithm in the literature. The second component is a parallelizable thresholding procedure THRESHOLDSEQ for adding elements with gain above a constant threshold. Finally, we demonstrate that our main algorithm empirically outperforms, in terms of runtime, adaptive rounds, total queries, and objective values, the previous state-of-the-art algorithm FAST in a comprehensive evaluation with six submodular objective functions.

Simultaenous Sieves: A Deterministic Streaming Algorithm for Non-Monotone Submodular Maximization

In this work, we present a combinatorial, deterministic single-pass streaming algorithm for the problem of maximizing a submodular function, not necessarily monotone, with respect to a cardinality constraint (SMCC). In the case the function is monotone, our algorithm reduces to the optimal streaming algorithm of Badanidiyuru et al. (2014). In general, our algorithm achieves ratio $\alpha / (1 + \alpha) - \varepsilon$, for any $\varepsilon > 0$, where $\alpha$ is the ratio of an offline (deterministic) algorithm for SMCC used for post-processing. Thus, if exponential computation time is allowed, our algorithm deterministically achieves nearly the optimal $1/2$ ratio. These results nearly match those of a recently proposed, randomized streaming algorithm that achieves the same ratios in expectation. For a deterministic, single-pass streaming algorithm, our algorithm achieves in polynomial time an improvement of the best approximation factor from $1/9$ of previous literature to $\approx 0.2689$.

Quick Streaming Algorithms for Maximization of Monotone Submodular Functions in Linear Time

We consider the problem of monotone, submodular maximization over a ground set of size $n$ subject to cardinality constraint $k$. For this problem, we introduce streaming algorithms with linearquery complexity and linear number of arithmetic operations; these algorithms are the first deterministic algorithms for submodular maximization that require a linear number of arithmetic operations. Specifically, for any $c \ge 1, \epsilon > 0$, we propose a single-pass, deterministic streaming algorithm with ratio $1/(4c)-\epsilon$, query complexity $\lceil n / c \rceil + c$, memory complexity $O(k \log k)$, and $O(n)$ total running time. As $k \to \infty$, the ratio converges to $(1 - 1/e)/(c + 1)$. In addition, we propose a deterministic, multi-pass streaming algorithm with $O(1 / \epsilon)$ passes that achieves ratio $1-1/e - \epsilon$ in $O(n/\epsilon)$ queries, $O(k \log (k))$ memory, and $O(n)$ time. We prove a lower bound that implies no constant-factor approximation exists using $o(n)$ queries, even if queries to infeasible sets are allowed. An experimental analysis demonstrates that our algorithms require fewer queries (often substantially less than $n$) to achieve better objective value than the current state-of-the-art algorithms.