DASH: Distributed Adaptive Sequencing Heuristic for Submodular Maximization

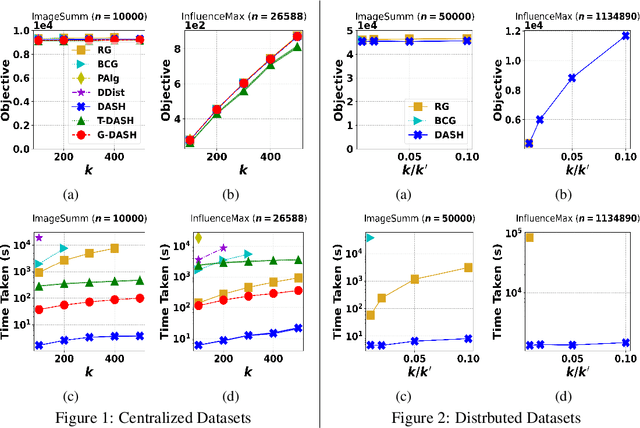
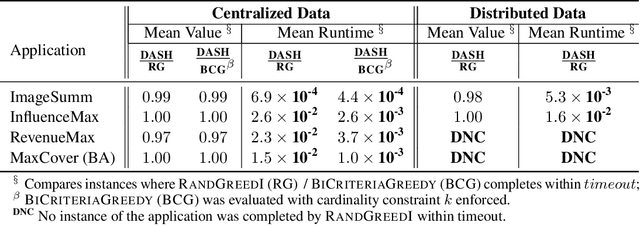
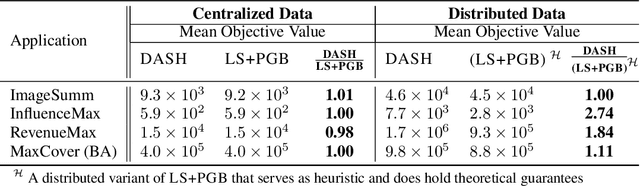
The development of parallelizable algorithms for monotone, submodular maximization subject to cardinality constraint (SMCC) has resulted in two separate research directions: centralized algorithms with low adaptive complexity, which require random access to the entire dataset; and distributed MapReduce (MR) model algorithms, that use a small number of MR rounds of computation. Currently, no MR model algorithm is known to use sublinear number of adaptive rounds which limits their practical performance. We study the SMCC problem in a distributed setting and present three separate MR model algorithms that introduce sublinear adaptivity in a distributed setup. Our primary algorithm, DASH achieves an approximation of $\frac{1}{2}(1-1/e-\varepsilon)$ using one MR round, while its multi-round variant METADASH enables MR model algorithms to be run on large cardinality constraints that were previously not possible. The two additional algorithms, T-DASH and G-DASH provide an improved ratio of ($\frac{3}{8}-\varepsilon$) and ($1-1/e-\varepsilon$) respectively using one and $(1/\varepsilon)$ MR rounds . All our proposed algorithms have sublinear adaptive complexity and we provide extensive empirical evidence to establish: DASH is orders of magnitude faster than the state-of-the-art distributed algorithms while producing nearly identical solution values; and validate the versatility of DASH in obtaining feasible solutions on both centralized and distributed data.