RELS-DQN: A Robust and Efficient Local Search Framework for Combinatorial Optimization

Combinatorial optimization (CO) aims to efficiently find the best solution to NP-hard problems ranging from statistical physics to social media marketing. A wide range of CO applications can benefit from local search methods because they allow reversible action over greedy policies. Deep Q-learning (DQN) using message-passing neural networks (MPNN) has shown promise in replicating the local search behavior and obtaining comparable results to the local search algorithms. However, the over-smoothing and the information loss during the iterations of message passing limit its robustness across applications, and the large message vectors result in memory inefficiency. Our paper introduces RELS-DQN, a lightweight DQN framework that exhibits the local search behavior while providing practical scalability. Using the RELS-DQN model trained on one application, it can generalize to various applications by providing solution values higher than or equal to both the local search algorithms and the existing DQN models while remaining efficient in runtime and memory.

DASH: Distributed Adaptive Sequencing Heuristic for Submodular Maximization

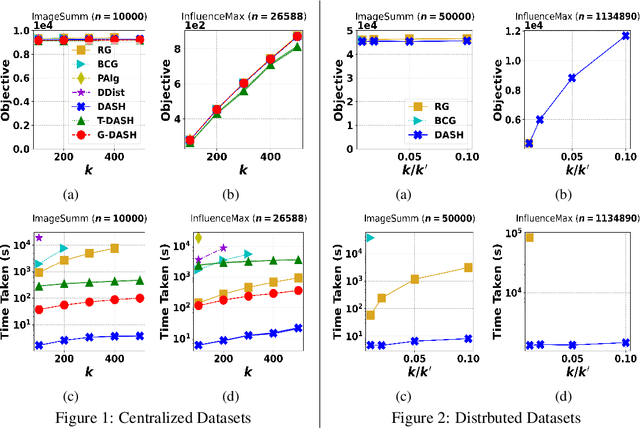
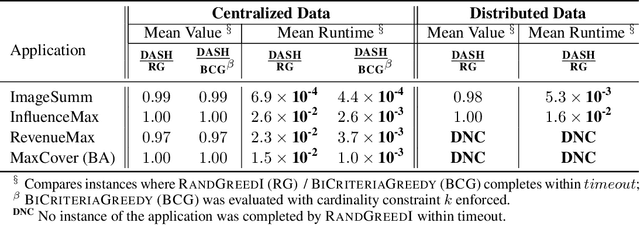
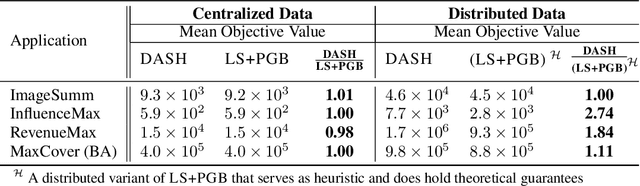
The development of parallelizable algorithms for monotone, submodular maximization subject to cardinality constraint (SMCC) has resulted in two separate research directions: centralized algorithms with low adaptive complexity, which require random access to the entire dataset; and distributed MapReduce (MR) model algorithms, that use a small number of MR rounds of computation. Currently, no MR model algorithm is known to use sublinear number of adaptive rounds which limits their practical performance. We study the SMCC problem in a distributed setting and present three separate MR model algorithms that introduce sublinear adaptivity in a distributed setup. Our primary algorithm, DASH achieves an approximation of $\frac{1}{2}(1-1/e-\varepsilon)$ using one MR round, while its multi-round variant METADASH enables MR model algorithms to be run on large cardinality constraints that were previously not possible. The two additional algorithms, T-DASH and G-DASH provide an improved ratio of ($\frac{3}{8}-\varepsilon$) and ($1-1/e-\varepsilon$) respectively using one and $(1/\varepsilon)$ MR rounds . All our proposed algorithms have sublinear adaptive complexity and we provide extensive empirical evidence to establish: DASH is orders of magnitude faster than the state-of-the-art distributed algorithms while producing nearly identical solution values; and validate the versatility of DASH in obtaining feasible solutions on both centralized and distributed data.

Best of Both Worlds: Practical and Theoretically Optimal Submodular Maximization in Parallel

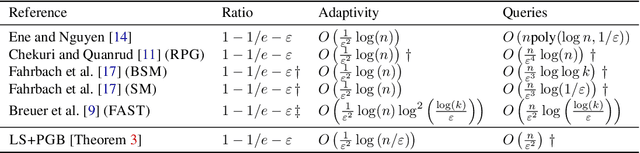
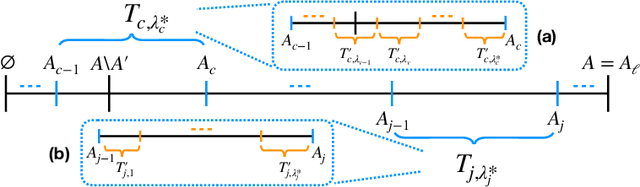
For the problem of maximizing a monotone, submodular function with respect to a cardinality constraint $k$ on a ground set of size $n$, we provide an algorithm that achieves the state-of-the-art in both its empirical performance and its theoretical properties, in terms of adaptive complexity, query complexity, and approximation ratio; that is, it obtains, with high probability, query complexity of $O(n)$ in expectation, adaptivity of $O(\log(n))$, and approximation ratio of nearly $1-1/e$. The main algorithm is assembled from two components which may be of independent interest. The first component of our algorithm, LINEARSEQ, is useful as a preprocessing algorithm to improve the query complexity of many algorithms. Moreover, a variant of LINEARSEQ is shown to have adaptive complexity of $O( \log (n / k) )$ which is smaller than that of any previous algorithm in the literature. The second component is a parallelizable thresholding procedure THRESHOLDSEQ for adding elements with gain above a constant threshold. Finally, we demonstrate that our main algorithm empirically outperforms, in terms of runtime, adaptive rounds, total queries, and objective values, the previous state-of-the-art algorithm FAST in a comprehensive evaluation with six submodular objective functions.