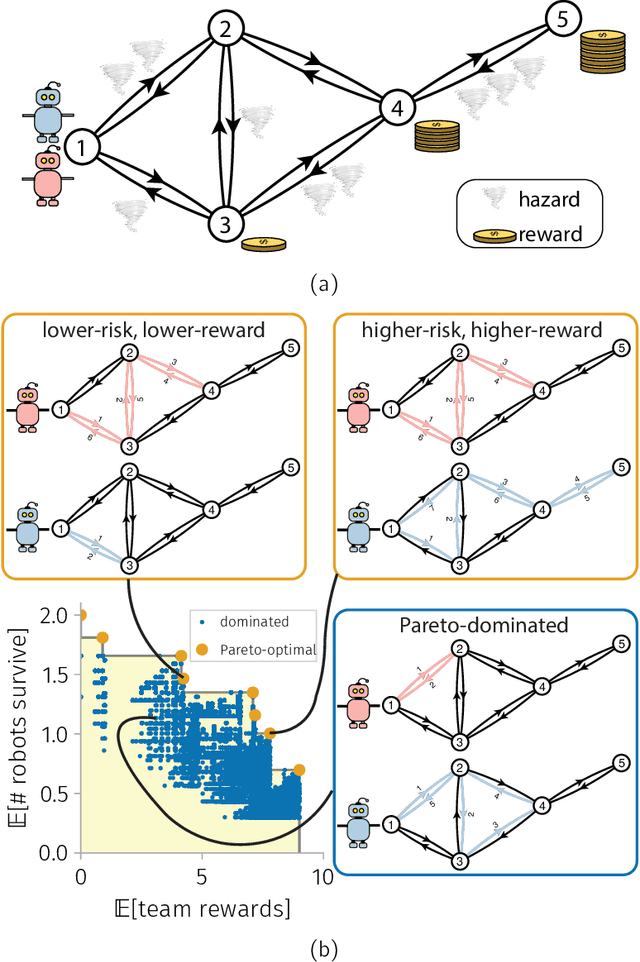
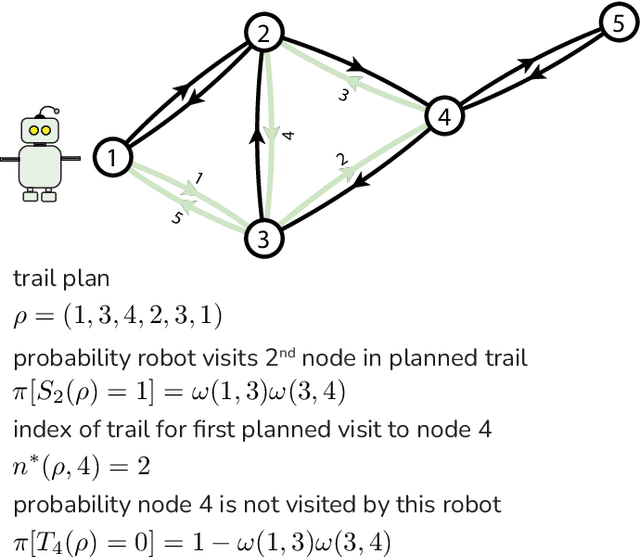
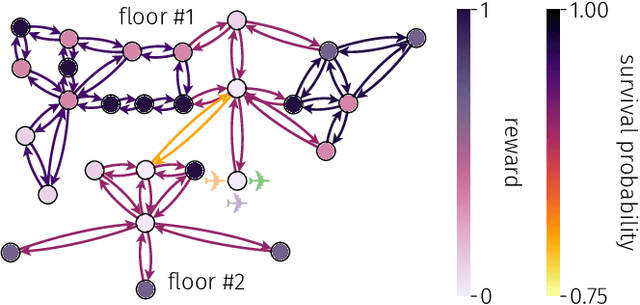
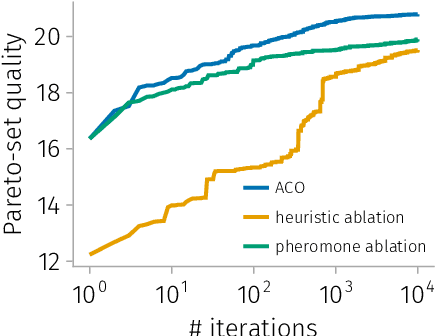
Bi-objective trail-planning for a robot team orienteering in a hazardous environment

Teams of mobile [aerial, ground, or aquatic] robots have applications in resource delivery, patrolling, information-gathering, agriculture, forest fire fighting, chemical plume source localization and mapping, and search-and-rescue. Robot teams traversing hazardous environments -- with e.g. rough terrain or seas, strong winds, or adversaries capable of attacking or capturing robots -- should plan and coordinate their trails in consideration of risks of disablement, destruction, or capture. Specifically, the robots should take the safest trails, coordinate their trails to cooperatively achieve the team-level objective with robustness to robot failures, and balance the reward from visiting locations against risks of robot losses. Herein, we consider bi-objective trail-planning for a mobile team of robots orienteering in a hazardous environment. The hazardous environment is abstracted as a directed graph whose arcs, when traversed by a robot, present known probabilities of survival. Each node of the graph offers a reward to the team if visited by a robot (which e.g. delivers a good to or images the node). We wish to search for the Pareto-optimal robot-team trail plans that maximize two [conflicting] team objectives: the expected (i) team reward and (ii) number of robots that survive the mission. A human decision-maker can then select trail plans that balance, according to their values, reward and robot survival. We implement ant colony optimization, guided by heuristics, to search for the Pareto-optimal set of robot team trail plans. As a case study, we illustrate with an information-gathering mission in an art museum.

Learning Strategic Value and Cooperation in Multi-Player Stochastic Games through Side Payments

For general-sum, n-player, strategic games with transferable utility, the Harsanyi-Shapley value provides a computable method to both 1) quantify the strategic value of a player; and 2) make cooperation rational through side payments. We give a simple formula to compute the HS value in normal-form games. Next, we provide two methods to generalize the HS values to stochastic (or Markov) games, and show that one of them may be computed using generalized Q-learning algorithms. Finally, an empirical validation is performed on stochastic grid-games with three or more players. Source code is provided to compute HS values for both the normal-form and stochastic game setting.