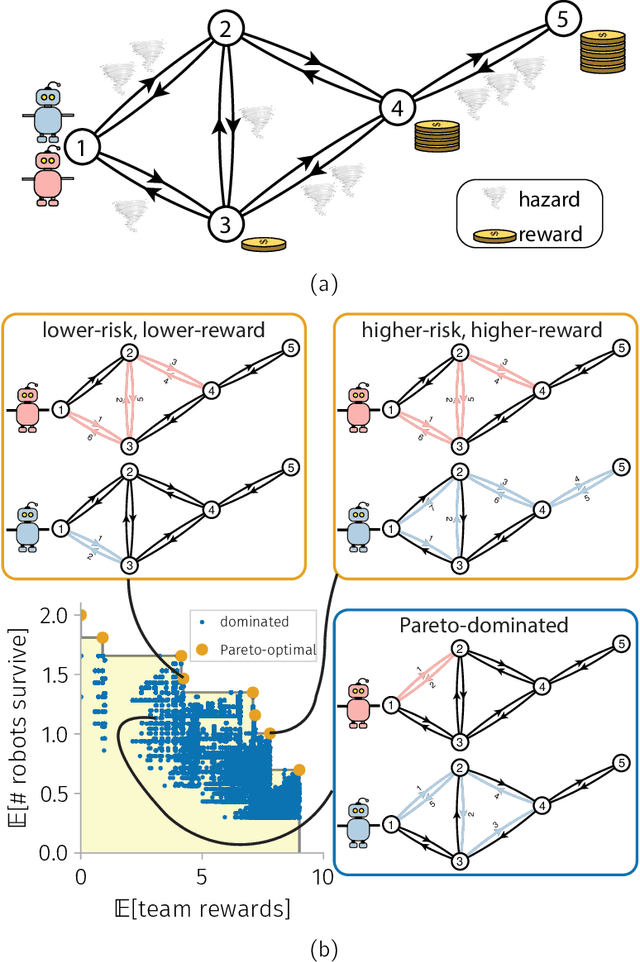
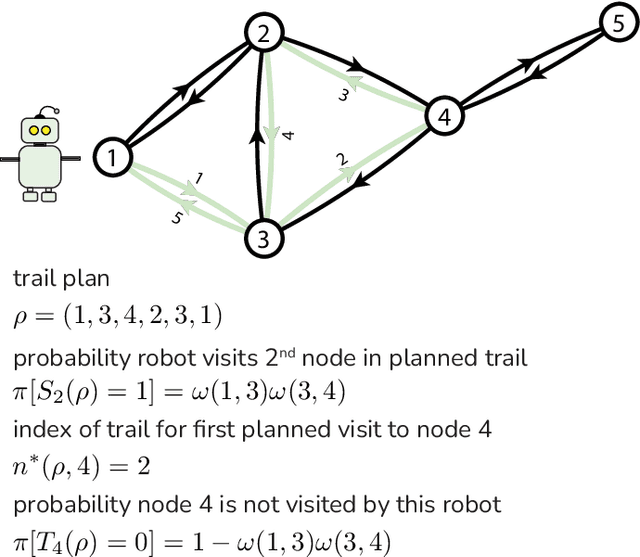
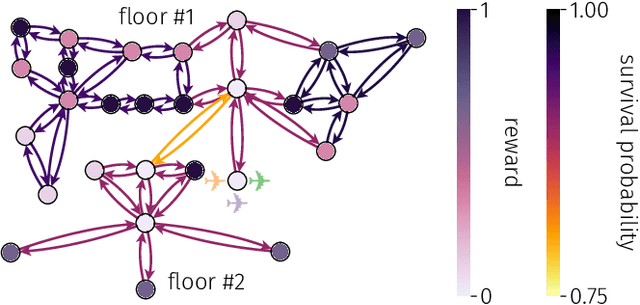
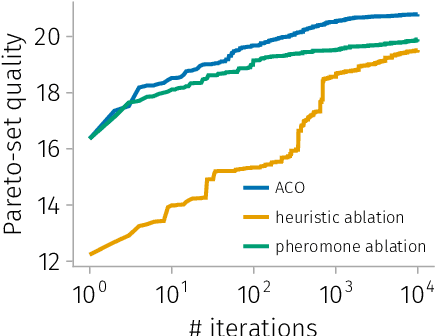
Bi-objective trail-planning for a robot team orienteering in a hazardous environment

Teams of mobile [aerial, ground, or aquatic] robots have applications in resource delivery, patrolling, information-gathering, agriculture, forest fire fighting, chemical plume source localization and mapping, and search-and-rescue. Robot teams traversing hazardous environments -- with e.g. rough terrain or seas, strong winds, or adversaries capable of attacking or capturing robots -- should plan and coordinate their trails in consideration of risks of disablement, destruction, or capture. Specifically, the robots should take the safest trails, coordinate their trails to cooperatively achieve the team-level objective with robustness to robot failures, and balance the reward from visiting locations against risks of robot losses. Herein, we consider bi-objective trail-planning for a mobile team of robots orienteering in a hazardous environment. The hazardous environment is abstracted as a directed graph whose arcs, when traversed by a robot, present known probabilities of survival. Each node of the graph offers a reward to the team if visited by a robot (which e.g. delivers a good to or images the node). We wish to search for the Pareto-optimal robot-team trail plans that maximize two [conflicting] team objectives: the expected (i) team reward and (ii) number of robots that survive the mission. A human decision-maker can then select trail plans that balance, according to their values, reward and robot survival. We implement ant colony optimization, guided by heuristics, to search for the Pareto-optimal set of robot team trail plans. As a case study, we illustrate with an information-gathering mission in an art museum.

A tutorial on the Bayesian statistical approach to inverse problems

Inverse problems are ubiquitous in the sciences and engineering. Two categories of inverse problems concerning a physical system are (1) estimate parameters in a model of the system from observed input-output pairs and (2) given a model of the system, reconstruct the input to it that caused some observed output. Applied inverse problems are challenging because a solution may (i) not exist, (ii) not be unique, or (iii) be sensitive to measurement noise contaminating the data. Bayesian statistical inversion (BSI) is an approach to tackle ill-posed and/or ill-conditioned inverse problems. Advantageously, BSI provides a "solution" that (i) quantifies uncertainty by assigning a probability to each possible value of the unknown parameter/input and (ii) incorporates prior information and beliefs about the parameter/input. Herein, we provide a tutorial of BSI for inverse problems, by way of illustrative examples dealing with heat transfer from ambient air to a cold lime fruit. First, we use BSI to infer a parameter in a dynamic model of the lime temperature from measurements of the lime temperature over time. Second, we use BSI to reconstruct the initial condition of the lime from a measurement of its temperature later in time. We demonstrate the incorporation of prior information, visualize the posterior distributions of the parameter/initial condition, and show posterior samples of lime temperature trajectories from the model. Our tutorial aims to reach a wide range of scientists and engineers.