Platonic Grounding for Efficient Multimodal Language Models

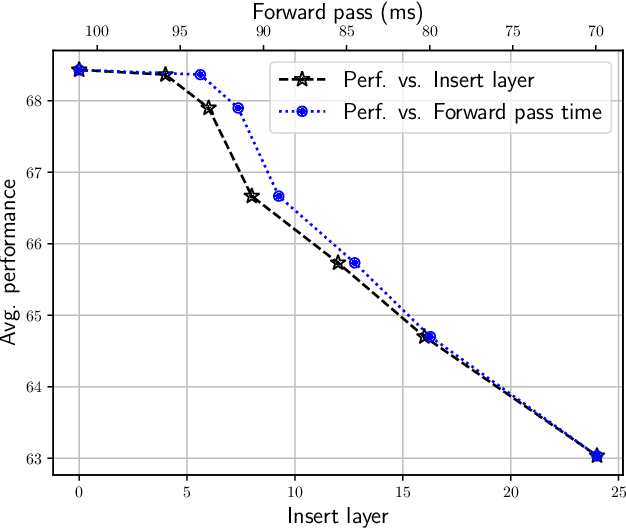
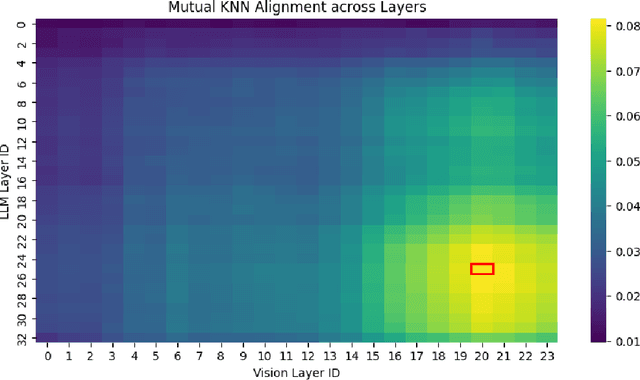
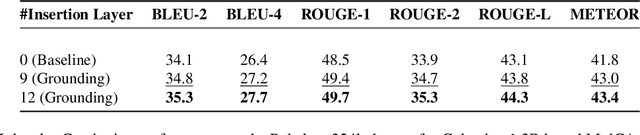
The hyperscaling of data and parameter count in Transformer-based models is yielding diminishing performance improvement, especially when weighed against training costs. Such plateauing indicates the importance of methods for more efficient finetuning and inference, while retaining similar performance. This is especially relevant for multimodal learning paradigms, where inference costs of processing multimodal tokens can determine the model's practical viability. At the same time, research on representations and mechanistic interpretability has improved our understanding of the inner workings of Transformer-based models; one such line of work reveals an implicit alignment in the deeper layers of pretrained models, across modalities. Taking inspiration from this, we motivate and propose a simple modification to existing multimodal frameworks that rely on aligning pretrained models. We demonstrate that our approach maintains and, in some cases, even improves performance of baseline methods while achieving significant gains in both training and inference-time compute. Our work also has implications for combining pretrained models into larger systems efficiently.

Fractional Budget Allocation for Influence Maximization under General Marketing Strategies

We consider the fractional influence maximization problem, i.e., identifying users on a social network to be incentivized with potentially partial discounts to maximize the influence on the network. The larger the discount given to a user, the higher the likelihood of its activation (adopting a new product or innovation), who then attempts to activate its neighboring users, causing a cascade effect of influence through the network. Our goal is to devise efficient algorithms that assign initial discounts to the network's users to maximize the total number of activated users at the end of the cascade, subject to a constraint on the total sum of discounts given. In general, the activation likelihood could be any non-decreasing function of the discount, whereas, our focus lies on the case when the activation likelihood is an affine function of the discount, potentially varying across different users. As this problem is shown to be NP-hard, we propose and analyze an efficient (1-1/e)-approximation algorithm. Furthermore, we run experiments on real-world social networks to show the performance and scalability of our method.