Identifiable Object-Centric Representation Learning via Probabilistic Slot Attention

Learning modular object-centric representations is crucial for systematic generalization. Existing methods show promising object-binding capabilities empirically, but theoretical identifiability guarantees remain relatively underdeveloped. Understanding when object-centric representations can theoretically be identified is crucial for scaling slot-based methods to high-dimensional images with correctness guarantees. To that end, we propose a probabilistic slot-attention algorithm that imposes an aggregate mixture prior over object-centric slot representations, thereby providing slot identifiability guarantees without supervision, up to an equivalence relation. We provide empirical verification of our theoretical identifiability result using both simple 2-dimensional data and high-resolution imaging datasets.

Vector Quantisation for Robust Segmentation

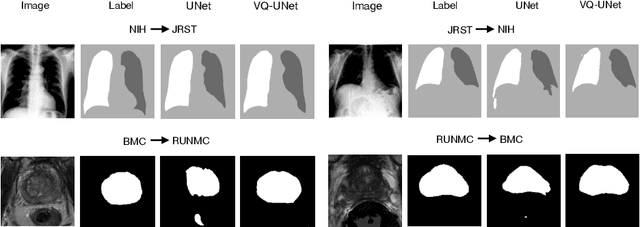
The reliability of segmentation models in the medical domain depends on the model's robustness to perturbations in the input space. Robustness is a particular challenge in medical imaging exhibiting various sources of image noise, corruptions, and domain shifts. Obtaining robustness is often attempted via simulating heterogeneous environments, either heuristically in the form of data augmentation or by learning to generate specific perturbations in an adversarial manner. We propose and justify that learning a discrete representation in a low dimensional embedding space improves robustness of a segmentation model. This is achieved with a dictionary learning method called vector quantisation. We use a set of experiments designed to analyse robustness in both the latent and output space under domain shift and noise perturbations in the input space. We adapt the popular UNet architecture, inserting a quantisation block in the bottleneck. We demonstrate improved segmentation accuracy and better robustness on three segmentation tasks. Code is available at \url{https://github.com/AinkaranSanthi/Vector-Quantisation-for-Robust-Segmentation}

Hierarchical Symbolic Reasoning in Hyperbolic Space for Deep Discriminative Models

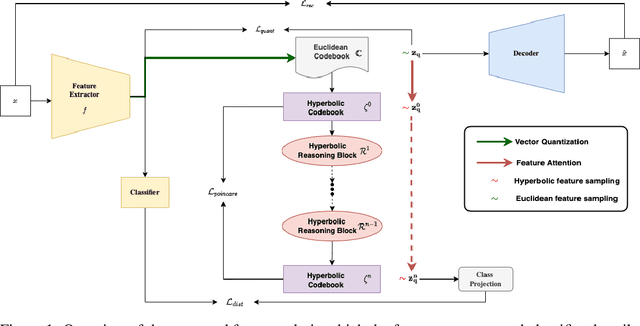
Explanations for \emph{black-box} models help us understand model decisions as well as provide information on model biases and inconsistencies. Most of the current explainability techniques provide a single level of explanation, often in terms of feature importance scores or feature attention maps in input space. Our focus is on explaining deep discriminative models at \emph{multiple levels of abstraction}, from fine-grained to fully abstract explanations. We achieve this by using the natural properties of \emph{hyperbolic geometry} to more efficiently model a hierarchy of symbolic features and generate \emph{hierarchical symbolic rules} as part of our explanations. Specifically, for any given deep discriminative model, we distill the underpinning knowledge by discretisation of the continuous latent space using vector quantisation to form symbols, followed by a \emph{hyperbolic reasoning block} to induce an \emph{abstraction tree}. We traverse the tree to extract explanations in terms of symbolic rules and its corresponding visual semantics. We demonstrate the effectiveness of our method on the MNIST and AFHQ high-resolution animal faces dataset. Our framework is available at \url{https://github.com/koriavinash1/SymbolicInterpretability}.