Getting Away with More Network Pruning: From Sparsity to Geometry and Linear Regions

One surprising trait of neural networks is the extent to which their connections can be pruned with little to no effect on accuracy. But when we cross a critical level of parameter sparsity, pruning any further leads to a sudden drop in accuracy. This drop plausibly reflects a loss in model complexity, which we aim to avoid. In this work, we explore how sparsity also affects the geometry of the linear regions defined by a neural network, and consequently reduces the expected maximum number of linear regions based on the architecture. We observe that pruning affects accuracy similarly to how sparsity affects the number of linear regions and our proposed bound for the maximum number. Conversely, we find out that selecting the sparsity across layers to maximize our bound very often improves accuracy in comparison to pruning as much with the same sparsity in all layers, thereby providing us guidance on where to prune.

Recall Distortion in Neural Network Pruning and the Undecayed Pruning Algorithm

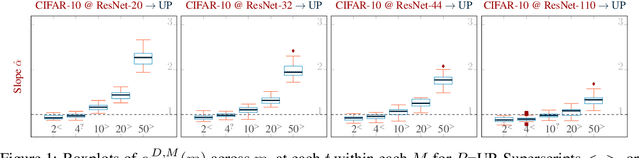
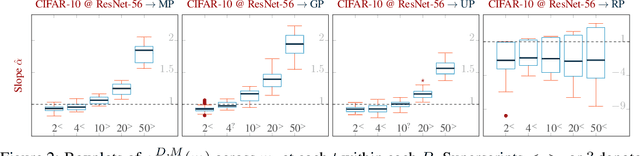
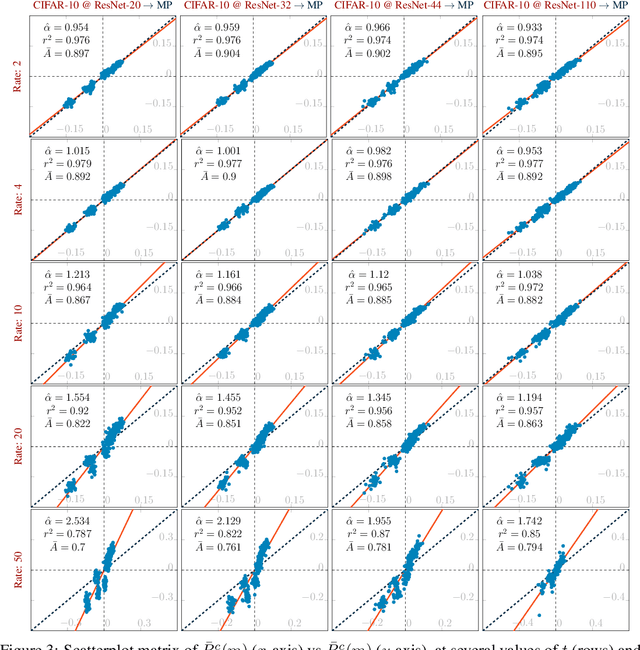
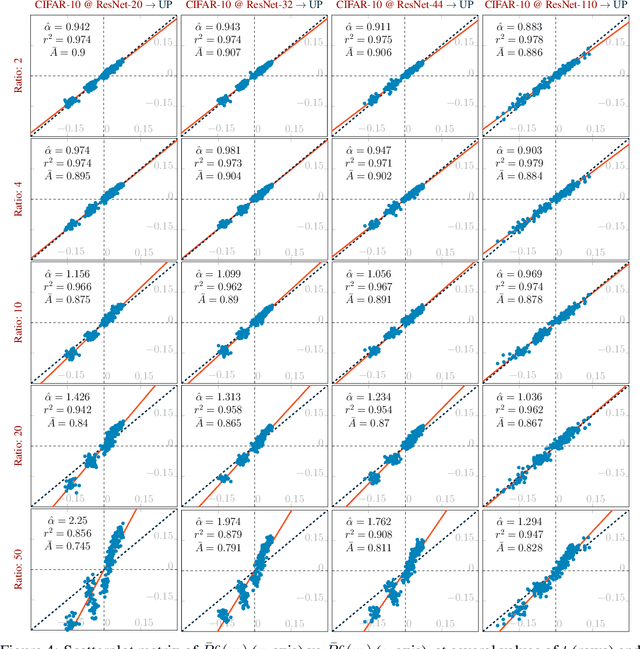
Pruning techniques have been successfully used in neural networks to trade accuracy for sparsity. However, the impact of network pruning is not uniform: prior work has shown that the recall for underrepresented classes in a dataset may be more negatively affected. In this work, we study such relative distortions in recall by hypothesizing an intensification effect that is inherent to the model. Namely, that pruning makes recall relatively worse for a class with recall below accuracy and, conversely, that it makes recall relatively better for a class with recall above accuracy. In addition, we propose a new pruning algorithm aimed at attenuating such effect. Through statistical analysis, we have observed that intensification is less severe with our algorithm but nevertheless more pronounced with relatively more difficult tasks, less complex models, and higher pruning ratios. More surprisingly, we conversely observe a de-intensification effect with lower pruning ratios.