Ahmed H. Elsheikh
DISTINGUISH Workflow: A New Paradigm of Dynamic Well Placement Using Generative Machine Learning
Mar 11, 2025Abstract:The real-time process of directional changes while drilling, known as geosteering, is crucial for hydrocarbon extraction and emerging directional drilling applications such as geothermal energy, civil infrastructure, and CO2 storage. The geo-energy industry seeks an automatic geosteering workflow that continually updates the subsurface uncertainties and captures the latest geological understanding given the most recent observations in real-time. We propose "DISTINGUISH": a real-time, AI-driven workflow designed to transform geosteering by integrating Generative Adversarial Networks (GANs) for geological parameterization, ensemble methods for model updating, and global discrete dynamic programming (DDP) optimization for complex decision-making during directional drilling operations. The DISTINGUISH framework relies on offline training of a GAN model to reproduce relevant geology realizations and a Forward Neural Network (FNN) to model Logging-While-Drilling (LWD) tools' response for a given geomodel. This paper introduces a first-of-its-kind workflow that progressively reduces GAN-geomodel uncertainty around and ahead of the drilling bit and adjusts the well plan accordingly. The workflow automatically integrates real-time LWD data with a DDP-based decision support system, enhancing predictive models of geology ahead of drilling and leading to better steering decisions. We present a simple yet representative benchmark case and document the performance target achieved by the DISTINGUISH workflow prototype. This benchmark will be a foundation for future methodological advancements and workflow refinements.
A Deep-Learning Iterative Stacked Approach for Prediction of Reactive Dissolution in Porous Media
Mar 11, 2025Abstract:Simulating reactive dissolution of solid minerals in porous media has many subsurface applications, including carbon capture and storage (CCS), geothermal systems and oil & gas recovery. As traditional direct numerical simulators are computationally expensive, it is of paramount importance to develop faster and more efficient alternatives. Deep-learning-based solutions, most of them built upon convolutional neural networks (CNNs), have been recently designed to tackle this problem. However, these solutions were limited to approximating one field over the domain (e.g. velocity field). In this manuscript, we present a novel deep learning approach that incorporates both temporal and spatial information to predict the future states of the dissolution process at a fixed time-step horizon, given a sequence of input states. The overall performance, in terms of speed and prediction accuracy, is demonstrated on a numerical simulation dataset, comparing its prediction results against state-of-the-art approaches, also achieving a speedup around $10^4$ over traditional numerical simulators.
Generating Infinite-Resolution Texture using GANs with Patch-by-Patch Paradigm
Sep 05, 2023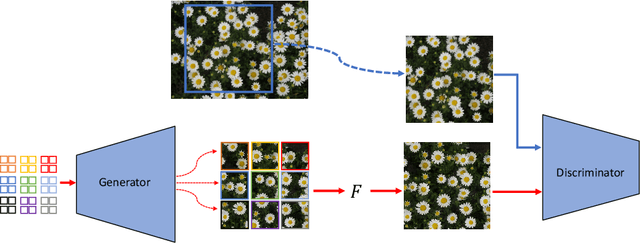
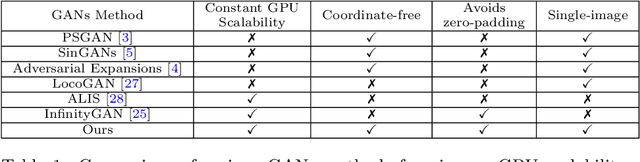
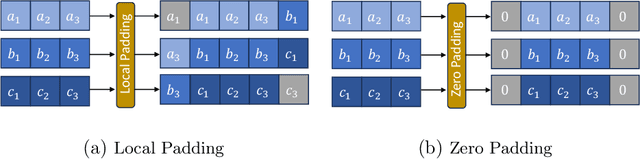

Abstract:In this paper, we introduce a novel approach for generating texture images of infinite resolutions using Generative Adversarial Networks (GANs) based on a patch-by-patch paradigm. Existing texture synthesis techniques often rely on generating a large-scale texture using a one-forward pass to the generating model, this limits the scalability and flexibility of the generated images. In contrast, the proposed approach trains GANs models on a single texture image to generate relatively small patches that are locally correlated and can be seamlessly concatenated to form a larger image while using a constant GPU memory footprint. Our method learns the local texture structure and is able to generate arbitrary-size textures, while also maintaining coherence and diversity. The proposed method relies on local padding in the generator to ensure consistency between patches and utilizes spatial stochastic modulation to allow for local variations and diversity within the large-scale image. Experimental results demonstrate superior scalability compared to existing approaches while maintaining visual coherence of generated textures.
Gym-preCICE: Reinforcement Learning Environments for Active Flow Control
May 03, 2023



Abstract:Active flow control (AFC) involves manipulating fluid flow over time to achieve a desired performance or efficiency. AFC, as a sequential optimisation task, can benefit from utilising Reinforcement Learning (RL) for dynamic optimisation. In this work, we introduce Gym-preCICE, a Python adapter fully compliant with Gymnasium (formerly known as OpenAI Gym) API to facilitate designing and developing RL environments for single- and multi-physics AFC applications. In an actor-environment setting, Gym-preCICE takes advantage of preCICE, an open-source coupling library for partitioned multi-physics simulations, to handle information exchange between a controller (actor) and an AFC simulation environment. The developed framework results in a seamless non-invasive integration of realistic physics-based simulation toolboxes with RL algorithms. Gym-preCICE provides a framework for designing RL environments to model AFC tasks, as well as a playground for applying RL algorithms in various AFC-related engineering applications.
Probabilistic forecasting for geosteering in fluvial successions using a generative adversarial network
Jul 04, 2022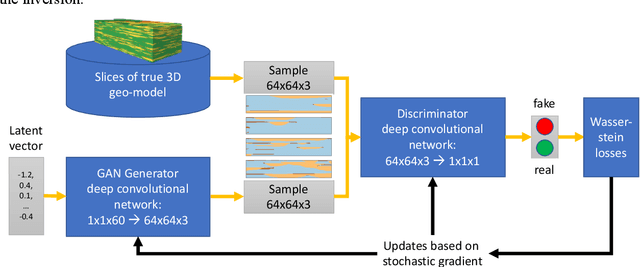
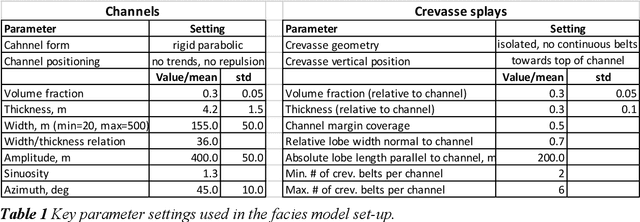
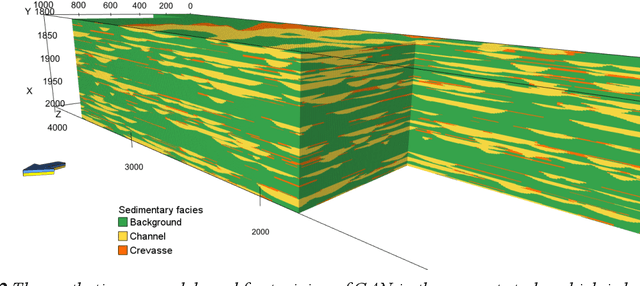
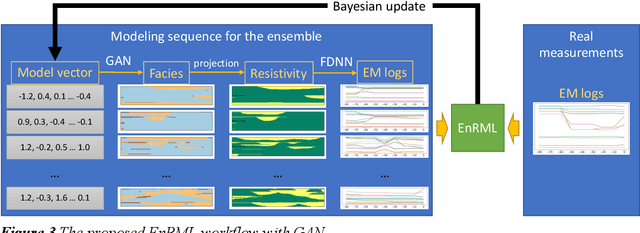
Abstract:Quantitative workflows utilizing real-time data to constrain ahead-of-bit uncertainty have the potential to improve geosteering significantly. Fast updates based on real-time data are essential when drilling in complex reservoirs with high uncertainties in pre-drill models. However, practical assimilation of real-time data requires effective geological modeling and mathematically robust parameterization. We propose a generative adversarial deep neural network (GAN), trained to reproduce geologically consistent 2D sections of fluvial successions. Offline training produces a fast GAN-based approximation of complex geology parameterized as a 60-dimensional model vector with standard Gaussian distribution of each component. Probabilistic forecasts are generated using an ensemble of equiprobable model vector realizations. A forward-modeling sequence, including a GAN, converts the initial (prior) ensemble of realizations into EM log predictions. An ensemble smoother minimizes statistical misfits between predictions and real-time data, yielding an update of model vectors and reduced uncertainty around the well. Updates can be then translated to probabilistic predictions of facies and resistivities. The present paper demonstrates a workflow for geosteering in an outcrop-based, synthetic fluvial succession. In our example, the method reduces uncertainty and correctly predicts most major geological features up to 500 meters ahead of drill-bit.
Generation of non-stationary stochastic fields using Generative Adversarial Networks with limited training data
May 11, 2022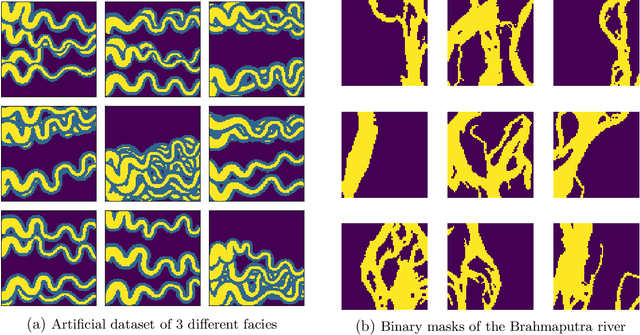
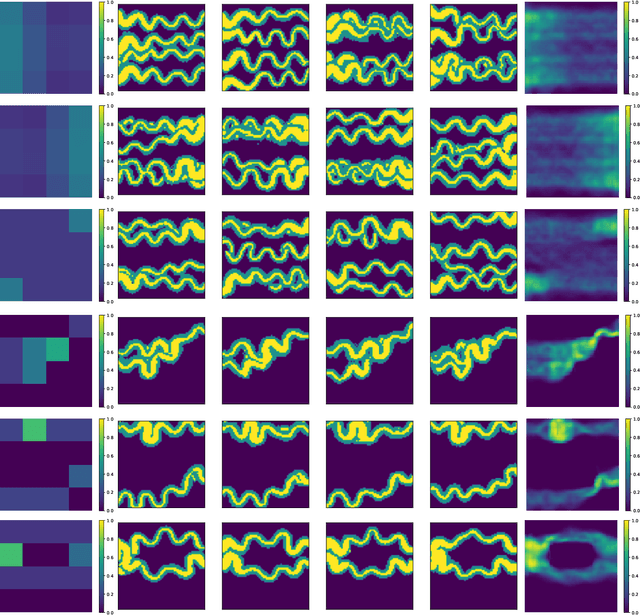
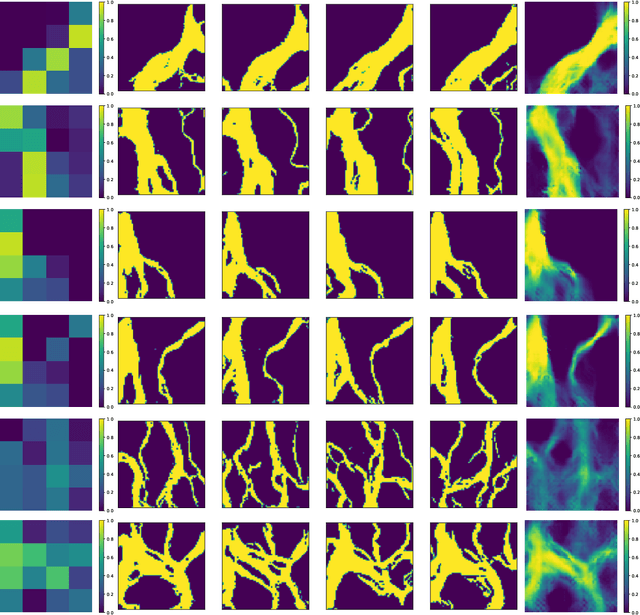
Abstract:In the context of generating geological facies conditioned on observed data, samples corresponding to all possible conditions are not generally available in the training set and hence the generation of these realizations depends primary on the generalization capability of the trained generative model. The problem becomes more complex when applied on non-stationary fields. In this work, we investigate the problem of training Generative Adversarial Networks (GANs) models against a dataset of geological channelized patterns that has a few non-stationary spatial modes and examine the training and self-conditioning settings that improve the generalization capability at new spatial modes that were never seen in the given training set. The developed training method allowed for effective learning of the correlation between the spatial conditions (i.e. non-stationary maps) and the realizations implicitly without using additional loss terms or solving a costly optimization problem at the realization generation phase. Our models, trained on real and artificial datasets were able to generate geologically-plausible realizations beyond the training samples with a strong correlation with the target maps.
Generating unrepresented proportions of geological facies using Generative Adversarial Networks
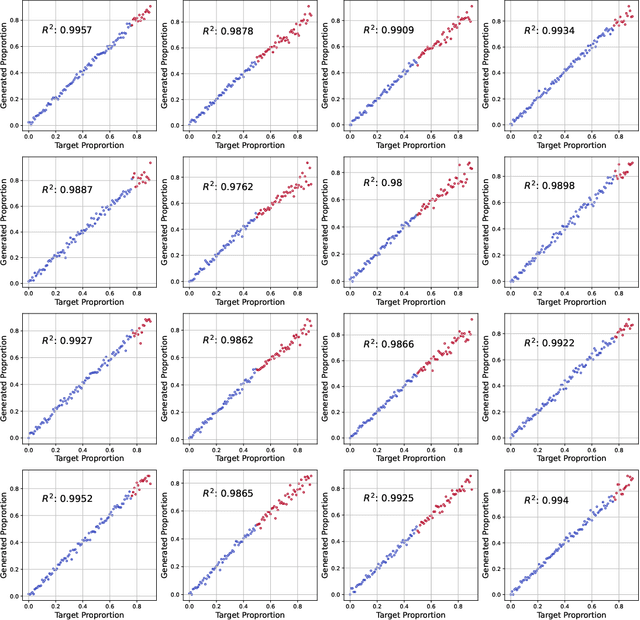
Mar 17, 2022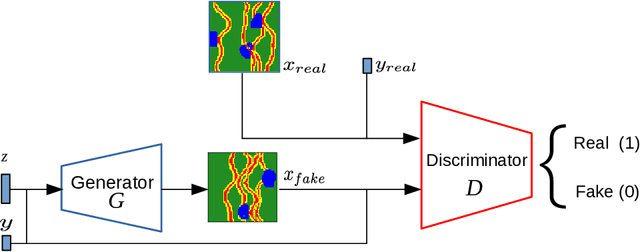



Abstract:In this work, we investigate the capacity of Generative Adversarial Networks (GANs) in interpolating and extrapolating facies proportions in a geological dataset. The new generated realizations with unrepresented (aka. missing) proportions are assumed to belong to the same original data distribution. Specifically, we design a conditional GANs model that can drive the generated facies toward new proportions not found in the training set. The presented study includes an investigation of various training settings and model architectures. In addition, we devised new conditioning routines for an improved generation of the missing samples. The presented numerical experiments on images of binary and multiple facies showed good geological consistency as well as strong correlation with the target conditions.
Optimal Bayesian experimental design for subsurface flow problems
Aug 10, 2020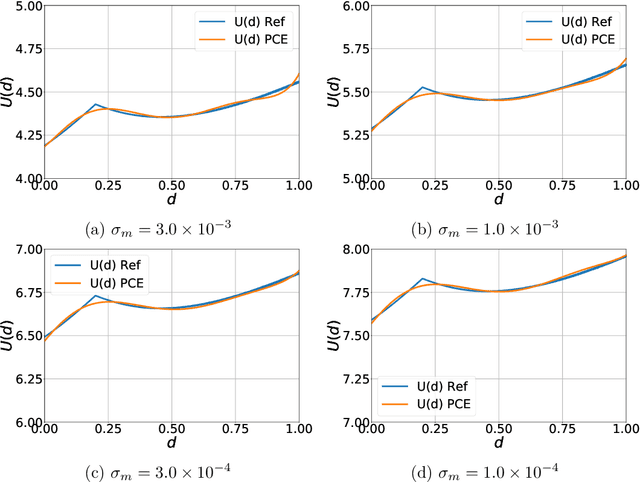
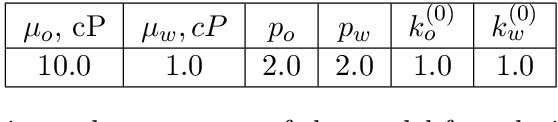
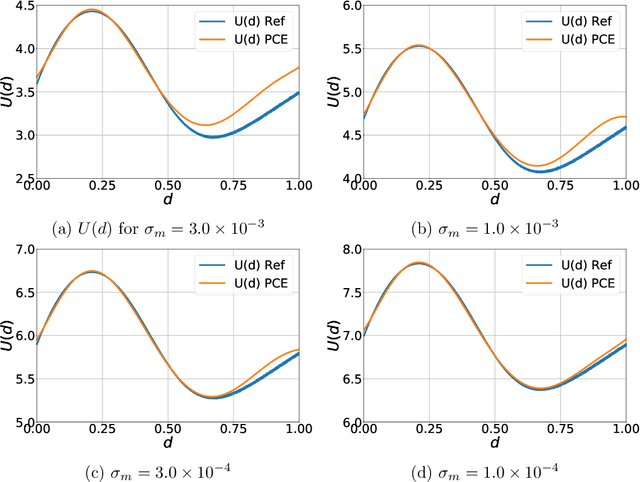
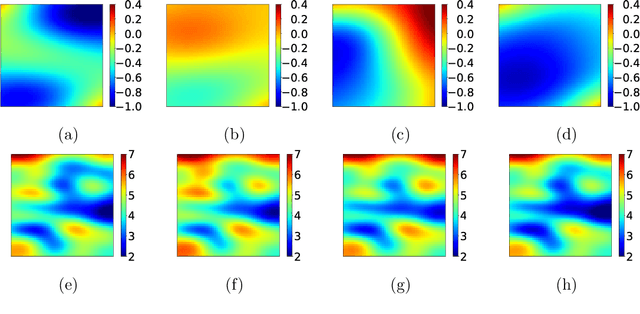
Abstract:Optimal Bayesian design techniques provide an estimate for the best parameters of an experiment in order to maximize the value of measurements prior to the actual collection of data. In other words, these techniques explore the space of possible observations and determine an experimental setup that produces maximum information about the system parameters on average. Generally, optimal Bayesian design formulations result in multiple high-dimensional integrals that are difficult to evaluate without incurring significant computational costs as each integration point corresponds to solving a coupled system of partial differential equations. In the present work, we propose a novel approach for development of polynomial chaos expansion (PCE) surrogate model for the design utility function. In particular, we demonstrate how the orthogonality of PCE basis polynomials can be utilized in order to replace the expensive integration over the space of possible observations by direct construction of PCE approximation for the expected information gain. This novel technique enables the derivation of a reasonable quality response surface for the targeted objective function with a computational budget comparable to several single-point evaluations. Therefore, the proposed technique reduces dramatically the overall cost of optimal Bayesian experimental design. We evaluate this alternative formulation utilizing PCE on few numerical test cases with various levels of complexity to illustrate the computational advantages of the proposed approach.
* 30 pages, 9 figures. Published in Computer Methods in Applied Mechanics and Engineering
Parametrization of stochastic inputs using generative adversarial networks with application in geology
Apr 09, 2019


Abstract:We investigate artificial neural networks as a parametrization tool for stochastic inputs in numerical simulations. We address parametrization from the point of view of emulating the data generating process, instead of explicitly constructing a parametric form to preserve predefined statistics of the data. This is done by training a neural network to generate samples from the data distribution using a recent deep learning technique called generative adversarial networks. By emulating the data generating process, the relevant statistics of the data are replicated. The method is assessed in subsurface flow problems, where effective parametrization of underground properties such as permeability is important due to the high dimensionality and presence of high spatial correlations. We experiment with realizations of binary channelized subsurface permeability and perform uncertainty quantification and parameter estimation. Results show that the parametrization using generative adversarial networks is very effective in preserving visual realism as well as high order statistics of the flow responses, while achieving a dimensionality reduction of two orders of magnitude.
Exemplar-based synthesis of geology using kernel discrepancies and generative neural networks
Sep 21, 2018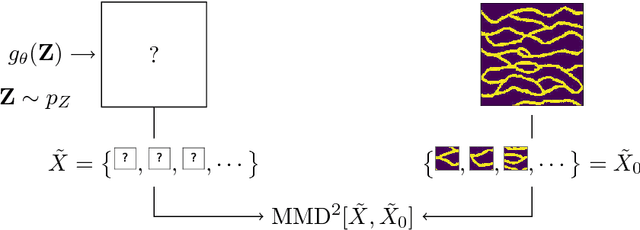


Abstract:We propose a framework for synthesis of geological images based on an exemplar image. We synthesize new realizations such that the discrepancy in the patch distribution between the realizations and the exemplar image is minimized. Such discrepancy is quantified using a kernel method for two-sample test called maximum mean discrepancy. To enable fast synthesis, we train a generative neural network in an offline phase to sample realizations efficiently during deployment, while also providing a parametrization of the synthesis process. We assess the framework on a classical binary image representing channelized subsurface reservoirs, finding that the method reproduces the visual patterns and spatial statistics (image histogram and two-point probability functions) of the exemplar image.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge