Digital Fingerprinting of Microstructures

Finding efficient means of fingerprinting microstructural information is a critical step towards harnessing data-centric machine learning approaches. A statistical framework is systematically developed for compressed characterisation of a population of images, which includes some classical computer vision methods as special cases. The focus is on materials microstructure. The ultimate purpose is to rapidly fingerprint sample images in the context of various high-throughput design/make/test scenarios. This includes, but is not limited to, quantification of the disparity between microstructures for quality control, classifying microstructures, predicting materials properties from image data and identifying potential processing routes to engineer new materials with specific properties. Here, we consider microstructure classification and utilise the resulting features over a range of related machine learning tasks, namely supervised, semi-supervised, and unsupervised learning. The approach is applied to two distinct datasets to illustrate various aspects and some recommendations are made based on the findings. In particular, methods that leverage transfer learning with convolutional neural networks (CNNs), pretrained on the ImageNet dataset, are generally shown to outperform other methods. Additionally, dimensionality reduction of these CNN-based fingerprints is shown to have negligible impact on classification accuracy for the supervised learning approaches considered. In situations where there is a large dataset with only a handful of images labelled, graph-based label propagation to unlabelled data is shown to be favourable over discarding unlabelled data and performing supervised learning. In particular, label propagation by Poisson learning is shown to be highly effective at low label rates.

Optimal Bayesian experimental design for subsurface flow problems

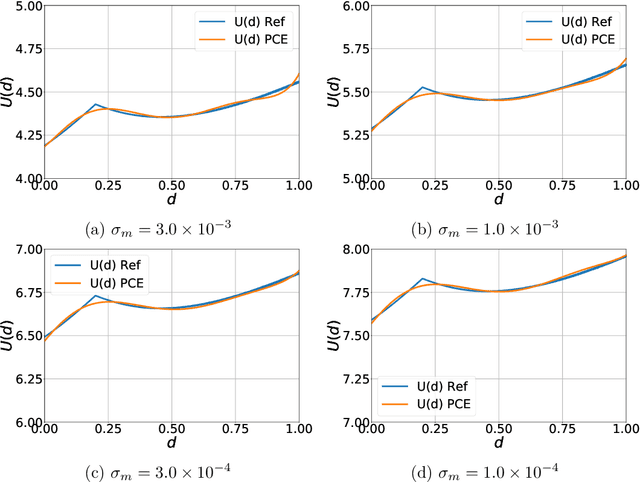
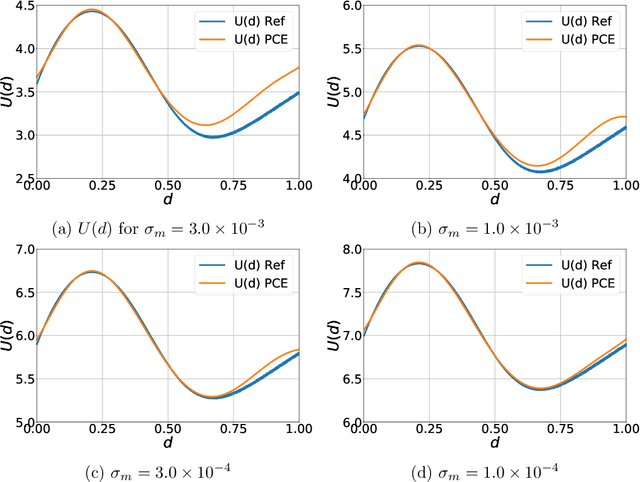
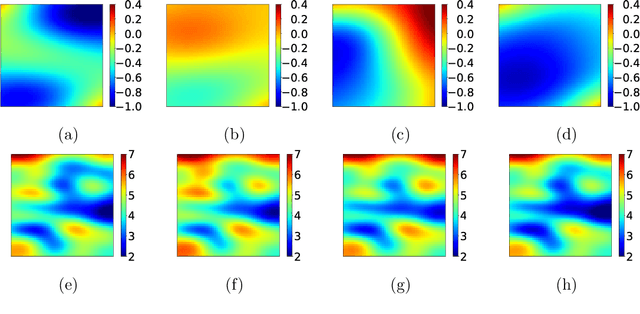
Optimal Bayesian design techniques provide an estimate for the best parameters of an experiment in order to maximize the value of measurements prior to the actual collection of data. In other words, these techniques explore the space of possible observations and determine an experimental setup that produces maximum information about the system parameters on average. Generally, optimal Bayesian design formulations result in multiple high-dimensional integrals that are difficult to evaluate without incurring significant computational costs as each integration point corresponds to solving a coupled system of partial differential equations. In the present work, we propose a novel approach for development of polynomial chaos expansion (PCE) surrogate model for the design utility function. In particular, we demonstrate how the orthogonality of PCE basis polynomials can be utilized in order to replace the expensive integration over the space of possible observations by direct construction of PCE approximation for the expected information gain. This novel technique enables the derivation of a reasonable quality response surface for the targeted objective function with a computational budget comparable to several single-point evaluations. Therefore, the proposed technique reduces dramatically the overall cost of optimal Bayesian experimental design. We evaluate this alternative formulation utilizing PCE on few numerical test cases with various levels of complexity to illustrate the computational advantages of the proposed approach.