Self-supervised Learning for Human Activity Recognition Using 700,000 Person-days of Wearable Data

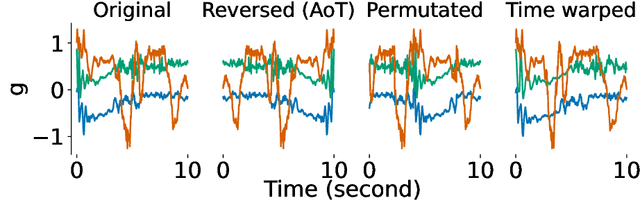
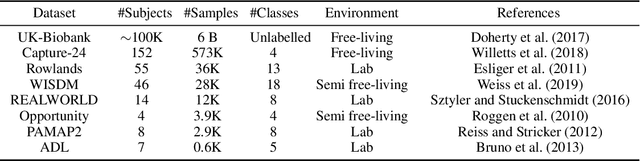
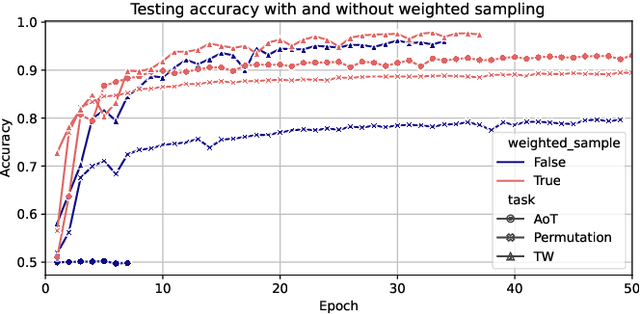
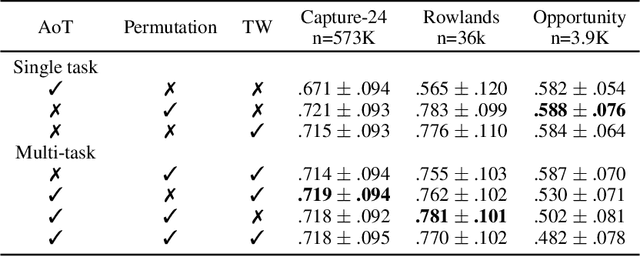
Advances in deep learning for human activity recognition have been relatively limited due to the lack of large labelled datasets. In this study, we leverage self-supervised learning techniques on the UK-Biobank activity tracker dataset--the largest of its kind to date--containing more than 700,000 person-days of unlabelled wearable sensor data. Our resulting activity recognition model consistently outperformed strong baselines across seven benchmark datasets, with an F1 relative improvement of 2.5%-100% (median 18.4%), the largest improvements occurring in the smaller datasets. In contrast to previous studies, our results generalise across external datasets, devices, and environments. Our open-source model will help researchers and developers to build customisable and generalisable activity classifiers with high performance.

Parametrization of stochastic inputs using generative adversarial networks with application in geology

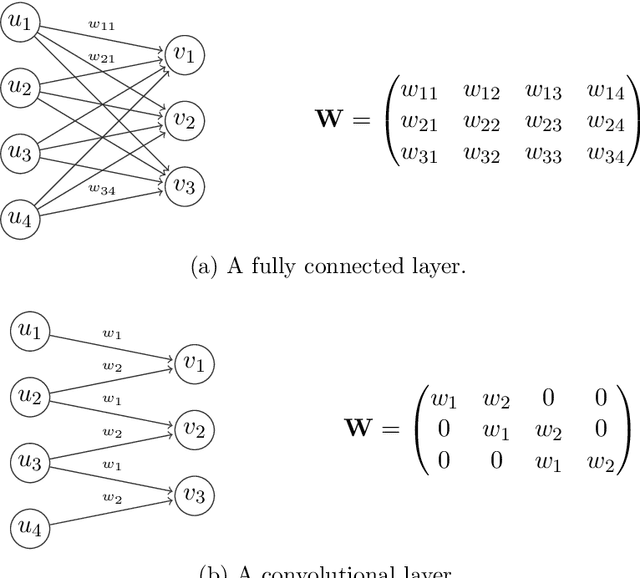
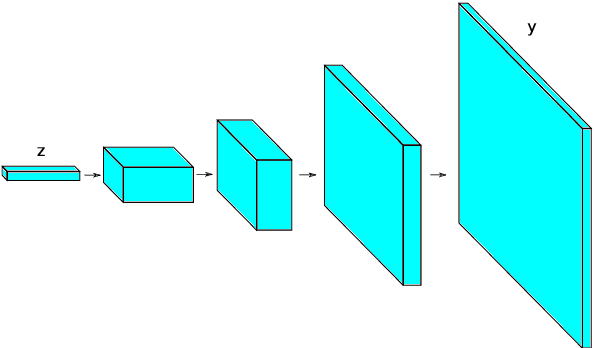
We investigate artificial neural networks as a parametrization tool for stochastic inputs in numerical simulations. We address parametrization from the point of view of emulating the data generating process, instead of explicitly constructing a parametric form to preserve predefined statistics of the data. This is done by training a neural network to generate samples from the data distribution using a recent deep learning technique called generative adversarial networks. By emulating the data generating process, the relevant statistics of the data are replicated. The method is assessed in subsurface flow problems, where effective parametrization of underground properties such as permeability is important due to the high dimensionality and presence of high spatial correlations. We experiment with realizations of binary channelized subsurface permeability and perform uncertainty quantification and parameter estimation. Results show that the parametrization using generative adversarial networks is very effective in preserving visual realism as well as high order statistics of the flow responses, while achieving a dimensionality reduction of two orders of magnitude.

Exemplar-based synthesis of geology using kernel discrepancies and generative neural networks

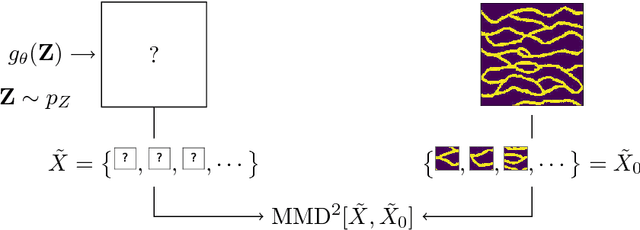
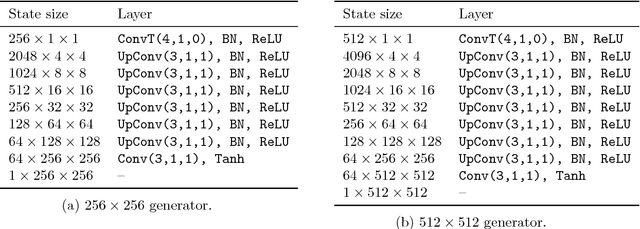
We propose a framework for synthesis of geological images based on an exemplar image. We synthesize new realizations such that the discrepancy in the patch distribution between the realizations and the exemplar image is minimized. Such discrepancy is quantified using a kernel method for two-sample test called maximum mean discrepancy. To enable fast synthesis, we train a generative neural network in an offline phase to sample realizations efficiently during deployment, while also providing a parametrization of the synthesis process. We assess the framework on a classical binary image representing channelized subsurface reservoirs, finding that the method reproduces the visual patterns and spatial statistics (image histogram and two-point probability functions) of the exemplar image.

Parametric generation of conditional geological realizations using generative neural networks

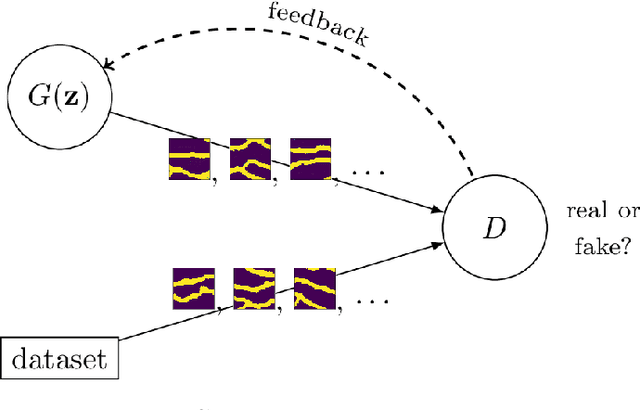
We introduce a method for parametric generation of conditional geological realizations using generative neural networks. We build on our recent work where we trained a neural network to generate unconditional geological realizations using generative adversarial networks. Here we propose a method for post-hoc conditioning of pre-trained generator networks to generate conditional realizations. We frame the problem in the Bayesian setting and model the posterior distribution of the latent vector given observations. To efficiently generate multiple latent vector solutions, we train a neural network to generate samples from the posterior distribution. This inference network is trained by minimizing the discrepancy between its output distribution and the posterior. Once the inference network is trained, it is coupled to the (unconditional) generator to obtain the conditional generator, thus also maintaining a parametrization of the (conditional) generation process.

A machine learning approach for efficient uncertainty quantification using multiscale methods

Several multiscale methods account for sub-grid scale features using coarse scale basis functions. For example, in the Multiscale Finite Volume method the coarse scale basis functions are obtained by solving a set of local problems over dual-grid cells. We introduce a data-driven approach for the estimation of these coarse scale basis functions. Specifically, we employ a neural network predictor fitted using a set of solution samples from which it learns to generate subsequent basis functions at a lower computational cost than solving the local problems. The computational advantage of this approach is realized for uncertainty quantification tasks where a large number of realizations has to be evaluated. We attribute the ability to learn these basis functions to the modularity of the local problems and the redundancy of the permeability patches between samples. The proposed method is evaluated on elliptic problems yielding very promising results.

Parametrization and Generation of Geological Models with Generative Adversarial Networks

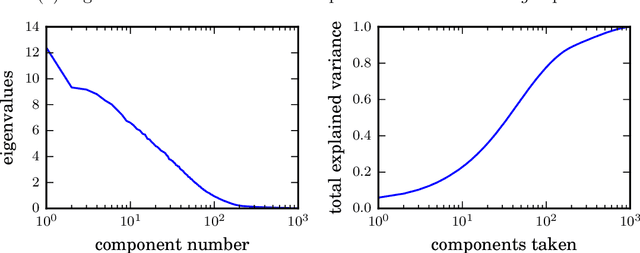
One of the main challenges in the parametrization of geological models is the ability to capture complex geological structures often observed in subsurface fields. In recent years, Generative Adversarial Networks (GAN) were proposed as an efficient method for the generation and parametrization of complex data, showing state-of-the-art performances in challenging computer vision tasks such as reproducing natural images (handwritten digits, human faces, etc.). In this work, we study the application of Wasserstein GAN for the parametrization of geological models. The effectiveness of the method is assessed for uncertainty propagation tasks using several test cases involving different permeability patterns and subsurface flow problems. Results show that GANs are able to generate samples that preserve the multipoint statistical features of the geological models both visually and quantitatively. The generated samples reproduce both the geological structures and the flow properties of the reference data.