The role of prior information and computational power in Machine Learning

Science consists on conceiving hypotheses, confronting them with empirical evidence, and keeping only hypotheses which have not yet been falsified. Under deductive reasoning they are conceived in view of a theory and confronted with empirical evidence in an attempt to falsify it, and under inductive reasoning they are conceived based on observation, confronted with empirical evidence and a theory is established based on the not falsified hypotheses. When the hypotheses testing can be performed with quantitative data, the confrontation can be achieved with Machine Learning methods, whose quality is highly dependent on the hypotheses' complexity, hence on the proper insertion of prior information into the set of hypotheses seeking to decrease its complexity without loosing good hypotheses. However, Machine Learning tools have been applied under the pragmatic view of instrumentalism, which is concerned only with the performance of the methods and not with the understanding of their behavior, leading to methods which are not fully understood. In this context, we discuss how prior information and computational power can be employed to solve a learning problem, but while prior information and a careful design of the hypotheses space has as advantage the interpretability of the results, employing high computational power has the advantage of a higher performance. We discuss why learning methods which combine both should work better from an understanding and performance perspective, arguing in favor of basic theoretical research on Machine Learning, in special about how properties of classifiers may be identified in parameters of modern learning models.

Learning the hypotheses space from data through a U-curve algorithm: a statistically consistent complexity regularizer for Model Selection

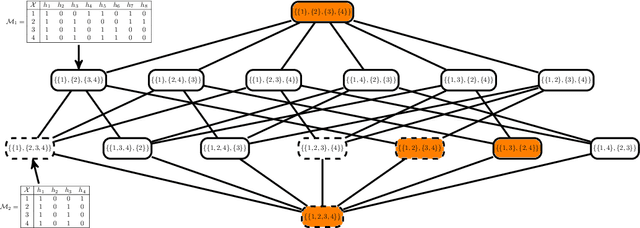
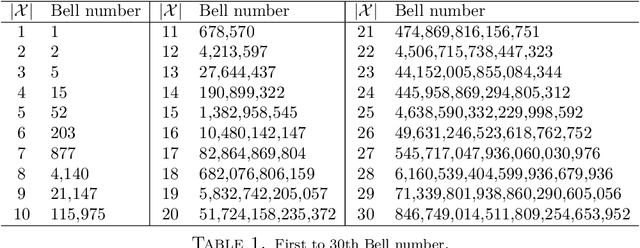
This paper proposes a data-driven systematic, consistent and non-exhaustive approach to Model Selection, that is an extension of the classical agnostic PAC learning model. In this approach, learning problems are modeled not only by a hypothesis space $\mathcal{H}$, but also by a Learning Space $\mathbb{L}(\mathcal{H})$, a poset of subspaces of $\mathcal{H}$, which covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, that is a suitable algebraic search space for Model Selection algorithms. Our main contributions are a data-driven general learning algorithm to perform regularized Model Selection on $\mathbb{L}(\mathcal{H})$ and a framework under which one can, theoretically, better estimate a target hypothesis with a given sample size by properly modeling $\mathbb{L}(\mathcal{H})$ and employing high computational power. A remarkable consequence of this approach are conditions under which a non-exhaustive search of $\mathbb{L}(\mathcal{H})$ can return an optimal solution. The results of this paper lead to a practical property of Machine Learning, that the lack of experimental data may be mitigated by a high computational capacity. In a context of continuous popularization of computational power, this property may help understand why Machine Learning has become so important, even where data is expensive and hard to get.

Learning the Hypotheses Space from data Part II: Convergence and Feasibility

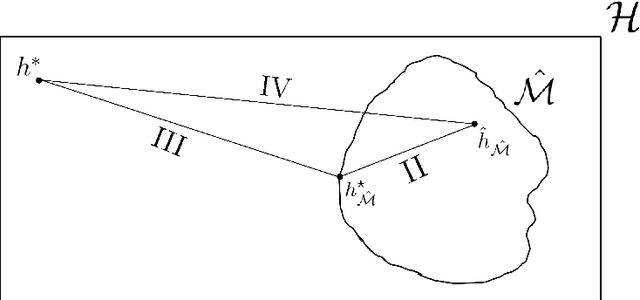
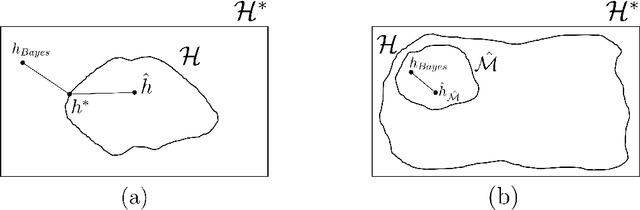
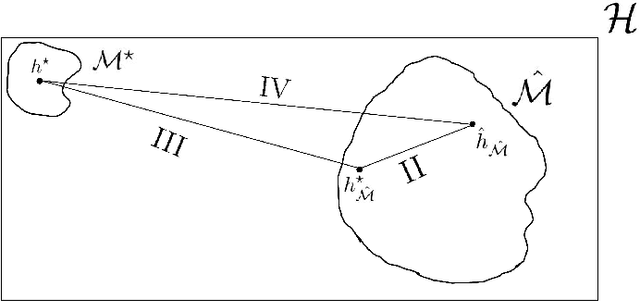
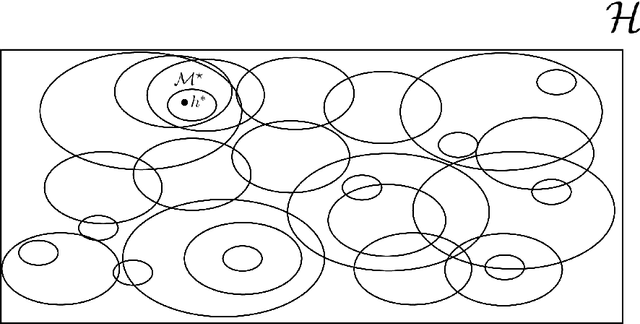
In part \textit{I} we proposed a structure for a general Hypotheses Space $\mathcal{H}$, the Learning Space $\mathbb{L}(\mathcal{H})$, which can be employed to avoid \textit{overfitting} when estimating in a complex space with relative shortage of examples. Also, we presented the U-curve property, which can be taken advantage of in order to select a Hypotheses Space without exhaustively searching $\mathbb{L}(\mathcal{H})$. In this paper, we carry further our agenda, by showing the consistency of a model selection framework based on Learning Spaces, in which one selects from data the Hypotheses Space on which to learn. The method developed in this paper adds to the state-of-the-art in model selection, by extending Vapnik-Chervonenkis Theory to \textit{random} Hypotheses Spaces, i.e., Hypotheses Spaces learned from data. In this framework, one estimates a random subspace $\hat{\mathcal{M}} \in \mathbb{L}(\mathcal{H})$ which converges with probability one to a target Hypotheses Space $\mathcal{M}^{\star} \in \mathbb{L}(\mathcal{H})$ with desired properties. As the convergence implies asymptotic unbiased estimators, we have a consistent framework for model selection, showing that it is feasible to learn the Hypotheses Space from data. Furthermore, we show that the generalization errors of learning on $\hat{\mathcal{M}}$ are lesser than those we commit when learning on $\mathcal{H}$, so it is more efficient to learn on a subspace learned from data.

Learning the Hypotheses Space from data Part I: Learning Space and U-curve Property

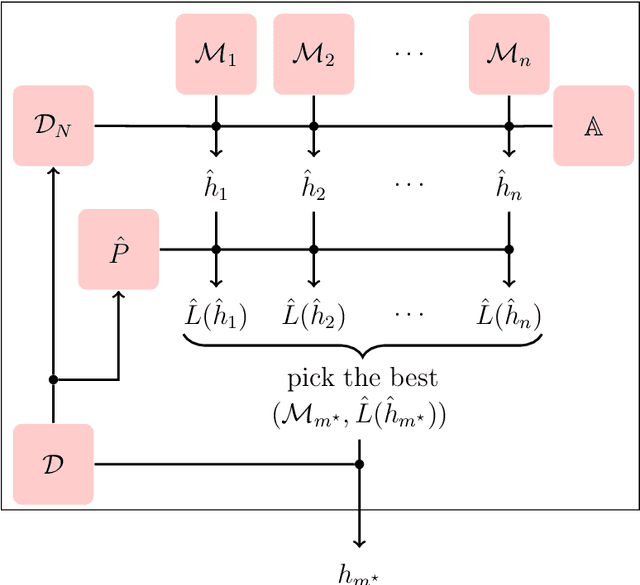
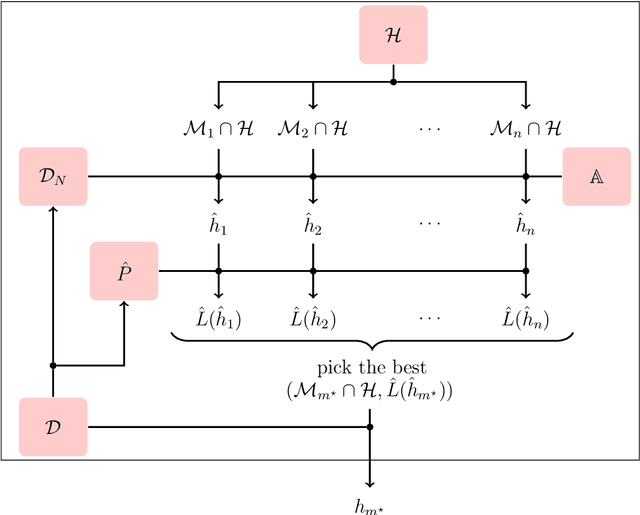
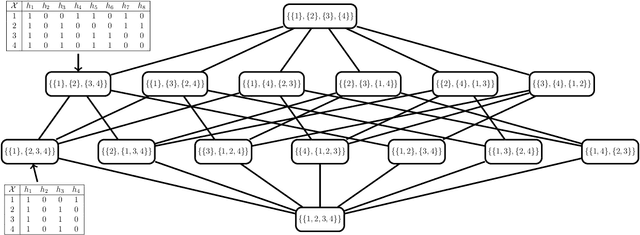
The agnostic PAC learning model consists of: a Hypothesis Space $\mathcal{H}$, a probability distribution $P$, a sample complexity function $m_{\mathcal{H}}(\epsilon,\delta): [0,1]^{2} \mapsto \mathbb{Z}_{+}$ of precision $\epsilon$ and confidence $1 - \delta$, a finite i.i.d. sample $\mathcal{D}_{N}$, a cost function $\ell$ and a learning algorithm $\mathbb{A}(\mathcal{H},\mathcal{D}_{N})$, which estimates $\hat{h} \in \mathcal{H}$ that approximates a target function $h^{\star} \in \mathcal{H}$ seeking to minimize out-of-sample error. In this model, prior information is represented by $\mathcal{H}$ and $\ell$, while problem solution is performed through their instantiation in several applied learning models, with specific algebraic structures for $\mathcal{H}$ and corresponding learning algorithms. However, these applied models use additional important concepts not covered by the classic PAC learning theory: model selection and regularization. This paper presents an extension of this model which covers these concepts. The main principle added is the selection, based solely on data, of a subspace of $\mathcal{H}$ with a VC-dimension compatible with the available sample. In order to formalize this principle, the concept of Learning Space $\mathbb{L}(\mathcal{H})$, which is a poset of subsets of $\mathcal{H}$ that covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, is presented as the natural search space for model selection algorithms. A remarkable result obtained on this new framework are conditions on $\mathbb{L}(\mathcal{H})$ and $\ell$ that lead to estimated out-of-sample error surfaces, which are true U-curves on $\mathbb{L}(\mathcal{H})$ chains, enabling a more efficient search on $\mathbb{L}(\mathcal{H})$. Hence, in this new framework, the U-curve optimization problem becomes a natural component of model selection algorithms.

Feature Selection based on the Local Lift Dependence Scale

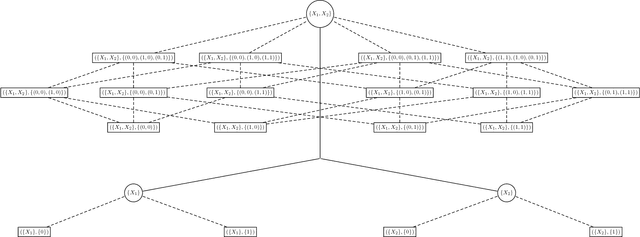
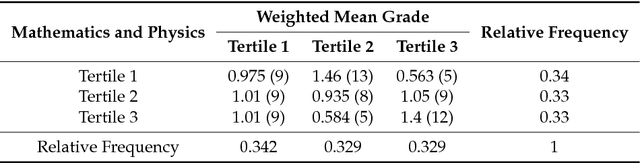
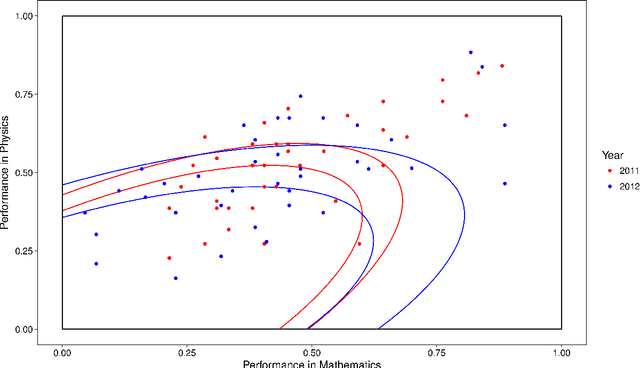
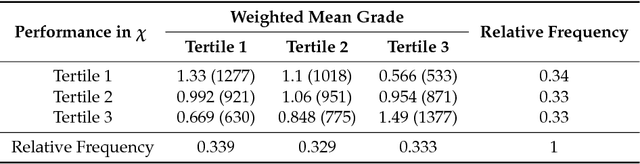
This paper uses a classical approach to feature selection: minimization of a cost function applied on estimated joint distributions. However, the search space in which such minimization is performed is extended. In the original formulation, the search space is the Boolean lattice of features sets (BLFS), while, in the present formulation, it is a collection of Boolean lattices of ordered pairs (features, associated value) (CBLOP), indexed by the elements of the BLFS. In this approach, we may not only select the features that are most related to a variable Y, but also select the values of the features that most influence the variable or that are most prone to have a specific value of Y. A local formulation of Shanon's mutual information is applied on a CBLOP to select features, namely, the Local Lift Dependence Scale, an scale for measuring variable dependence in multiple resolutions. The main contribution of this paper is to define and apply this local measure, which permits to analyse local properties of joint distributions that are neglected by the classical Shanon's global measure. The proposed approach is applied to a dataset consisting of student performances on a university entrance exam, as well as on undergraduate courses. The approach is also applied to two datasets of the UCI Machine Learning Repository.